���㣺�ȱȹ�ϵ��ȷ��,�Ȳ��ϵ��ȷ��,���е����
ר�⣺�Ȳ�������ȱ�����
��������1�����4�ס��黯���С�{a
n}��������ȣ���a
1+a
2+a
3+a
4=0������ȣ��ٽ��|a
1|+|a
2|+|a
3|+|a
4|=1�����������еĸ������
��2������Ȳ����еĹ�����a
1+a
2+a
3+��+a
11=0�ɵ�a
6=0��Ȼ��ֹ������0����С��0���������ʽ����������Ȳ����е�ͨ�ʽ����
��3���ɹ黯���ж����֪{a
n}������������ĺ͵���
�����и�����ĺ͵���
-��Ȼ�����÷�����֤�����������IJ���ʽ��
���
��1���⣺��a
1��a
2��a
3��a
4�ɹ���Ϊq�ĵȱ����У���Ȼq��1������a
1+a
2+a
3+a
4=0��
��
=0�����q=-1��
��|a
1|+|a
2|+|a
3|+|a
4|=1����4|a
1|=1�����
a1=����
������
��-����-��
-����-��Ϊ�����Ľס��黯���С���
��2���⣺��Ȳ�����a
1��a
2��a
3������a
11�Ĺ���Ϊd��
��a
1+a
2+a
3+��+a
11=0���ã�
11a1+=0��
��a
1+5d=0����a
6=0��
��d=0ʱ����黯���е�������ì�ܣ�
��d��0ʱ����
a1+a2+��+a5=-��a6=0���ã�
�����
d=��a1=-��
��
an=-+=(n��N*��n��11)��
��d��0ʱ����
a1+a2+��+a5=��a6=0���ã�
�����
d=-��a1=��
��
an=-=-��n��N
*��n��11����
��
an=��n��N
*��n��11����
��3��֤��������֪��֪������a
i��0��Ҳ����a
j��0��i��j��{1��2������n����i��j����
��
ai1��ai2������aip��a
i�������0������
aj1��aj2������ajm��a
i��������0������
����֪��X=
ai1+ai2+��+aip=��Y=
aj1+aj2+��+ajm=-��
��
a1+a2+��+an=
| p |
 |
| k=1 |
+| m |
 |
| k=1 |
��| p |
 |
| k=1 |
aik+| m |
 |
| k=1 |
ajk=-��
���������⿼��Ȳ��ϵ�͵ȱȹ�ϵ��ȷ���������˵ȱ����к͵Ȳ�����ͨ�ʽ����ѵ���˷�����֤������ʽ��������Ĺؼ��Ƕ��¶��塰�黯���С������⣬���е��⣮







 ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
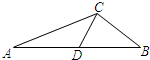 ��ͼ���ڡ�ABC�У�|
��ͼ���ڡ�ABC�У�|