已知函数f(x)=x3+2x2+x.
(I)求函数f(x)的单调区间与极值;
(II)若对于任意x∈(0,+∞),f(x)≥ax2恒成立,求实数a的取值范围.
解:(I)∵f'(x)=3x
2+4x+1=(3x+1)(x+1)
令f'(x)>0得x>-

或x<-1
故函数在(-∞,-1)与(-

,+∞)是增函数,在(-1,-

)是减函数,故函数在x=-1处取到极大值,在x=-

处取到极小值
极大值为0,极小值-

(II)若对于任意x∈(0,+∞),f(x)≥ax
2恒成立,则必有a≤
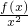
=x+

+2对于任意x∈(0,+∞),恒成立,
∵x+

+2≥4,等号当且仅当x=

=1时成立
∴a≤4
∴实数a的取值范围(-∞,4]
分析:(Ⅰ)先求出函数的导数,再令导数大于0求出单调增区间,导数小于0求出函数的减区间,再由极值的定义判断出极值即可;
(II)若对于任意x∈(0,+∞),f(x)≥ax
2恒成立,则必有a≤
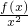
对于任意x∈(0,+∞),恒成立,易求.
点评:本题考查利用导数研究函数的极值以及由函数恒成立的问题求参数的取值范围,求解本题关键是记忆好求导的公式以及极值的定义,对于函数的恒成立的问题求参数,要注意正确转化,恰当的转化可以大大降低解题难度.

 或x<-1
或x<-1 ,+∞)是增函数,在(-1,-
,+∞)是增函数,在(-1,- )是减函数,故函数在x=-1处取到极大值,在x=-
)是减函数,故函数在x=-1处取到极大值,在x=- 处取到极小值
处取到极小值
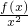 =x+
=x+ +2对于任意x∈(0,+∞),恒成立,
+2对于任意x∈(0,+∞),恒成立, +2≥4,等号当且仅当x=
+2≥4,等号当且仅当x= =1时成立
=1时成立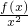 对于任意x∈(0,+∞),恒成立,易求.
对于任意x∈(0,+∞),恒成立,易求.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<