练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．在△ABC中，“$\overrightarrow{CA}•\overrightarrow{CB}＞0$”，是“△ABC为锐角三角形”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    分析 在△ABC中，“$\overrightarrow{CA}•\overrightarrow{CB}＞0$”?C为锐角，根据充要条件的定义，可得答案．

    解答 解：在△ABC中，
    ∵“$\overrightarrow{CA}•\overrightarrow{CB}＞0$”?$\left|\overrightarrow{CA}\right|•\left|\overrightarrow{CB}\right|•cosC＞0$?cosC＞0?C为锐角，
    故，“$\overrightarrow{CA}•\overrightarrow{CB}＞0$”，是“△ABC为锐角三角形”的必要不充分条件，
    故选：B．

    点评 本题考查的知识点是平面向量的数量积的运算，充要条件，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．过点（-2，0）且在两坐标轴上的截距之差为3的直线方程是5x+2y+10=0，或x-2y+2=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知命题p：“关于x，y的方程x2-2ax+y2+2a2-5a+4=0（a∈R）表示圆”，命题q：“?x∈R，使得x2+（a-1）x+1＞0（a∈R）恒成立”．
    （1）若命题p为真命题，求实数a的取值范围；
    （2）若命题p∧q为真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．各项均为正数的数列{an}的前n次和Sn，已知S1=2，a7=20，且2（a+b）Sn=（an+a）（an+b），n∈N+，b＞$\frac{3}{2}$＞a．
    （1）求a和b的值；
    （2）bn=$\frac{{a}_{n}+1}{3•{2}^{n}}$，记数列{bn}的前n项和为Tn，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

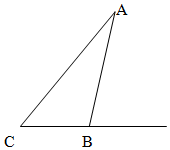    9．如图为了立一块广告牌，要制造一个三角形的支架   三角形支架形状如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了广告牌稳固，要求AC的长度越短越好，则AC最短为2+$\sqrt{3}$米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．过点（-1，3）且与直线2x+y+3=0垂直的直线方程为（　　）
    A．x-2y+7=0B．2x-y+5=0C．x-2y-5=0D．2x+y-5=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，且点P（2，1）在椭圆C上．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若点A、B都在椭圆C上，且AB中点M在线段OP（不包括端点）上．求△AOB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知F1、F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过F2作双曲线渐近线的垂线，垂足为P，若|PF1|2-|PF2|2=c2．则双曲线离心率的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设数列{an}前n项和为Sn
    （1）若an=2n+1，则Sn=n2+2n，
    （2）若an+Sn=1，则Sn的取值范围是[$\frac{1}{2}$，1）．

    查看答案和解析>>

    同步练习册答案