
如图所示,平面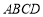
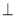 平面
平面 ,且四边形
,且四边形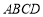 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
,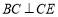 ,
, ,
, .
.
(1)求证
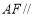 平面
平面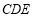 ;(2)求平面
;(2)求平面 与平面
与平面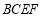 所成锐二面角的余弦值.
所成锐二面角的余弦值.

(1)证明见解析;(2)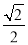 .
.
【解析】
试题分析:(方法一:传统几何方法)(1)证明线面平行,可在平面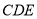 内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明
内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明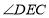 为平面
为平面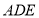 与平面
与平面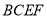 所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.
所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.
(方法二:空间向量方法)(1)本小题可以以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立空间直角坐标系,把问题转化为证明AF的方向向量与平面CDE的一个法向量垂直(证它们的数量积为零),而根据题意易得这个法向量为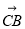 ;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量
;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量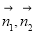 ,利用公式
,利用公式 完成计算即可,但要注意本题面面角为锐二面角.
完成计算即可,但要注意本题面面角为锐二面角.
试题解析:(方法一:)(1)取CE中点为G,连接DG,FG,
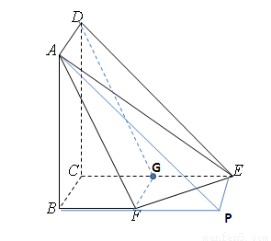
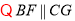 且
且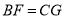 ,∴四边形BFGC为平行四边形,则
,∴四边形BFGC为平行四边形,则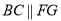 且
且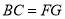 .
.
∵四边形ABCD为矩形,∴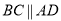 且
且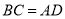 ,∴
,∴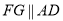 且
且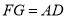 ,
,
∴四边形AFGD为平行四边形,则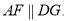
∵ ,
, ,∴
,∴ .
.
(2)过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,
∵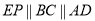 ,∴A,P,E,D四点共面.
,∴A,P,E,D四点共面. 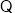 四边形
四边形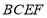 为直角梯形,四边形
为直角梯形,四边形 为矩形,
为矩形,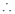
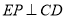 ,
,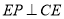 ,又
,又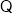
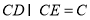 ,
, 平面
平面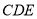 ,
,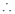
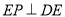 ,又
,又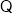 平面
平面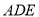
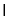 平面
平面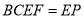 ,
,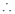
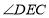 为平面
为平面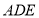 与平面
与平面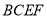 所成锐二面角的平面角.
所成锐二面角的平面角.
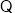
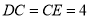 ,
,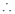
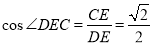 .即平面
.即平面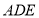 与平面
与平面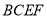 所成锐二面角的余弦值为
所成锐二面角的余弦值为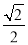 .
.
(方法二:)(1)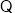 四边形
四边形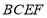 为直角梯形,四边形
为直角梯形,四边形 为矩形,
为矩形,
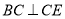 ,
,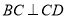 ,又
,又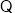 平面
平面
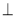 平面
平面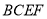 ,且平面
,且平面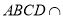 平面
平面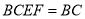 ,∴
,∴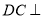 平面
平面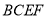 ,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.
,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.
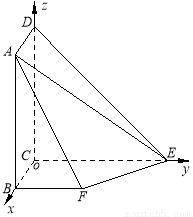
根据题意我们可得以下点的坐标: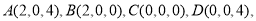
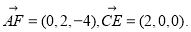
∵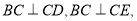 ∴
∴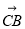 为平面
为平面 的一个法向量,又∵
的一个法向量,又∵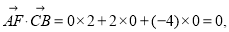
∴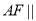 平面
平面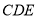 .
.
(2)设平面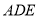 的一个法向量为
的一个法向量为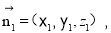 则
则 ,∵
,∵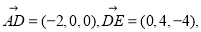

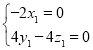 , 取
, 取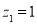 ,得
,得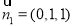 .
.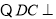 平面
平面 ,
,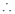 平面
平面 一个法向量为
一个法向量为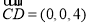 ,设平面
,设平面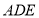 与平面
与平面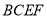 所成锐二面角的大小为
所成锐二面角的大小为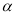 ,则
,则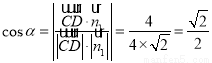 .因此,平面
.因此,平面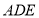 与平面
与平面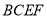 所成锐二面角的余弦值为
所成锐二面角的余弦值为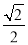 .
.
考点:线面平行的判定定理,二面角及其平面角的定义,二面角的余弦公式,向量的数量积,空间直角坐标系的建立及坐标的找寻,法向量的求法.


科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
点P在正方体ABCD﹣A1B1C1D1的底面ABCD所在平面上,E是A1A的中点,且∠EPA=∠D1PD,则点P的轨迹是( )
A.直线 B.圆 C.抛物线 D.双曲线
查看答案和解析>>
科目:高中数学 来源:2015届浙江省金华十校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
函数f(x)=2sinxcosx是( )
A.最小正周期为2π的奇函数
B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数
D.最小正周期为π的偶函数
查看答案和解析>>
科目:高中数学 来源:2015届浙江省绍兴市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知 的内角A,B,C所对的边分别为a,b,c,若
的内角A,B,C所对的边分别为a,b,c,若 的可能取值为( ).
的可能取值为( ).
A.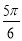 B.
B.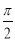 C.
C. D.
D.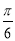
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期期中文科数学试卷(解析版) 题型:选择题
现有四个函数:①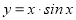 ;②
;②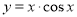 ;③
;③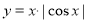 ; ④
; ④ 的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
的图象(部分)如下,但顺序被打乱,则按照从左到右将图象对应的函数序号安排正确的一组是( )
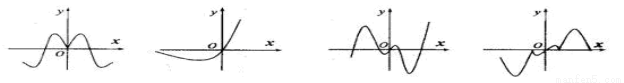
A.④①②③ B.①④③② C.①④②③ D.③④②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com