
分析 (1)先由y=2x2,得y′=4x.当x=-1时,y'=-4.由此能求出l1的方程.由y=2x2及x=a,解得点B的坐标为(a,2a2).由4x+y+2=0及x=a,解得点D的坐标为(a,-4a-2).点A到直线BD的距离为|a+1|.由此能求出S1的值.(2)当a>-1时,S1=(a+1)3,利用积分求出S2,知S1:S2的值为与a无关的常数.
解答 解:(1)由y=2x2,得y'=4x.当x=-1时,y'=-4.
∴l1的方程为y-2=-4(x+1),即4x+y+2=0.
由y=2x2及x=a,解得点B的坐标为(a,2a2).
由4x+y+2=0及x=a,解得点D的坐标为(a,-4a-2).
又可求得点A到直线BD的距离为|a+1|,|BD|=2a2+4a+2=2(a+1)2.
∴S1=|a+1|3.…..(6分)
(2)由题意,当a>-1时,S1=(a+1)3,
${S_2}=\int_{-1}^a{(2{x^2}+4x+2)dx=(\frac{2}{3}{x^3}+2{x^2}+2x)\left|{_{-1}^a}\right.}$
=$\frac{2}{3}{a^3}+2{a^2}+2a+\frac{2}{3}-2+2=\frac{2}{3}{(a+1)^3}$,
当a<-1时,${S_2}=\int_a^{-1}{(2{x^2}+4x+2)dx}$=$-\frac{2}{3}{(a+1)^3}$,
∴S1:S2=3:2.…..(12分)
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意双曲线的性质、导数、定积分的灵活运用,合理地进行等价转化.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 命题“?x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是a≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
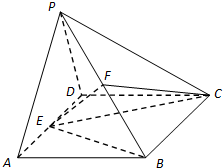 如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.
如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com