
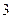 次;在
次;在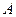 处每投进一球得
处每投进一球得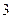 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过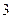 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在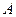 处的命中率
处的命中率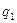 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在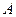 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3  | P4 |
 的值;
的值;  的数学期望E
的数学期望E .
.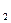 =0.8;
=0.8; 
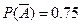 , P(B)= q
, P(B)= q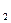 ,
, .
. =0时
=0时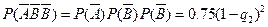 =0.03,
=0.03,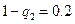 ,q
,q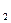 =0.8.………………………………
=0.8.……………………………… ….3分
….3分 =2时, P1=
=2时, P1=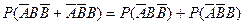 ……………………….5分
……………………….5分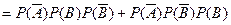 =0.75
=0.75 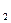 (
(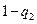 )×2=1.5 q
)×2=1.5 q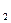 (
(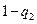 )=0.24
)=0.24 =3
=3 时, P2 =
时, P2 =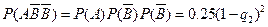 =0.01, ………….7分
=0.01, ………….7分 =4时, P3=
=4时, P3=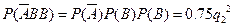 =0.48, …………………….9分
=0.48, …………………….9分 =5时, P4=
=5时, P4=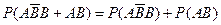
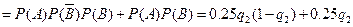 =0.24……………………11分
=0.24……………………11分 的分布列为
的分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
 的数学期望
的数学期望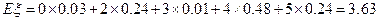


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源:不详 题型:解答题
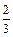 ,每次考科目B成绩合格的概率均为
,每次考科目B成绩合格的概率均为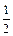 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为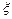 .
.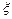 的分布列和期望
的分布列和期望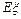 ;
; 书的概率.
书的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 若小张参加每次考核合格的概率依次组成一个公差为
若小张参加每次考核合格的概率依次组成一个公差为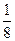 的等差数列,他参加第一次考核合格的概率超过
的等差数列,他参加第一次考核合格的概率超过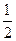 ,且他直到参加第二次考核才合格的概率为
,且他直到参加第二次考核才合格的概率为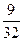
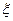 和分布列和数学期望值
和分布列和数学期望值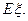
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与产量
与产量 的函数关系式为
的函数关系式为
 与产量
与产量 的函数关系式如下表所示:
的函数关系式如下表所示:| 市场情形 | 概率 | 价格 与产量 与产量 的函数关系式 的函数关系式 |
| 好 | 0.4 |  |
| 中 | 0.4 |  |
| 差 | 0.2 |  |
 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润. 与产量
与产量 的函数关系式;
的函数关系式; 确定时,求期望
确定时,求期望 ;
; 取何值时,
取何值时, 取得最大值.
取得最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 如下:若是白色,则
如下:若是白色,则 ;若是黄色,则
;若是黄色,则 ;若是红色,则
;若是红色,则 ;若卡片数字是
;若卡片数字是 ,则
,则

 与数字方差
与数字方差
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。 为射手射击3次后的总的分数,求
为射手射击3次后的总的分数,求 的分布列。
的分布列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的观测值过程如下:
的观测值过程如下: ;类比甲的算法试计算语文
;类比甲的算法试计算语文 的观测值是多少?(精确0.1)
的观测值是多少?(精确0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com