
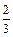 ,每次考科目B成绩合格的概率均为
,每次考科目B成绩合格的概率均为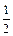 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为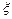 .
.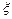 的分布列和期望
的分布列和期望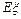 ;
; 书的概率.
书的概率. 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
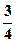 、
、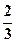 、
、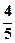 。已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场。
。已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场。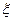 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求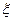 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
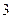 次;在
次;在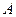 处每投进一球得
处每投进一球得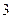 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过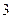 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在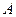 处的命中率
处的命中率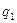 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为  | 0 | 2 | 3 | 4 | 5 |
| p | 0.03 | P1 | P2 | P3  | P4 |
 的值;
的值;  的数学期望E
的数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题:
时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题: 的分布列和期望;
的分布列和期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
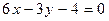 ,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,
,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,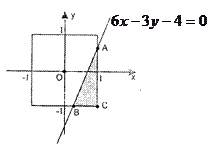
A.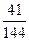 | B.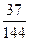 | C.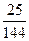 | D.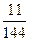 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com