
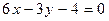 ,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,
,向边长为2的正方形内随机地投飞镖,飞镖都能投入正方形内,且投到每个点的可能性相等,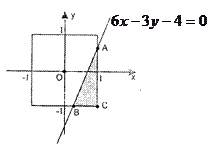
A.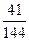 | B.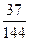 | C.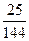 | D.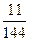 |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:不详 题型:解答题
 奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
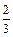 ,每次考科目B成绩合格的概率均为
,每次考科目B成绩合格的概率均为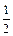 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试的次数为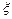 .
.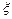 的分布列和期望
的分布列和期望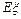 ;
; 书的概率.
书的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与产量
与产量 的函数关系式为
的函数关系式为
 与产量
与产量 的函数关系式如下表所示:
的函数关系式如下表所示:| 市场情形 | 概率 | 价格 与产量 与产量 的函数关系式 的函数关系式 |
| 好 | 0.4 |  |
| 中 | 0.4 |  |
| 差 | 0.2 |  |
 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量 ,表示当产量为
,表示当产量为 ,而市场前景无法确定的利润.
,而市场前景无法确定的利润. 与产量
与产量 的函数关系式;
的函数关系式; 确定时,求期望
确定时,求期望 ;
; 取何值时,
取何值时, 取得最大值.
取得最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
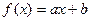 ,
,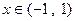 ,
,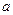 、
、 是常数.
是常数.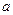 是从
是从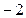 、
、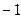 、
、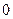 、
、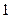 、
、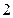 五个数中任取的一个数,
五个数中任取的一个数,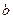 是从
是从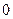 、
、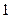 、
、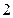 三个数中任取的一个数,求函数
三个数中任取的一个数,求函数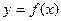 为奇函数的概率.
为奇函数的概率.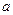 是从区间
是从区间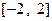 中任取的一个数,
中任取的一个数,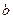 是从区间
是从区间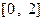 中任取的一个数,求函数
中任取的一个数,求函数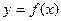 有零点的概率.
有零点的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元,求
元,求 的概率分布列和数学期望.
的概率分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的观测值过程如下:
的观测值过程如下: ;类比甲的算法试计算语文
;类比甲的算法试计算语文 的观测值是多少?(精确0.1)
的观测值是多少?(精确0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com