
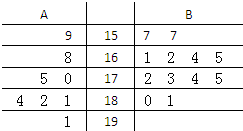
 ij��ʦ������������ϡ����A��B�������ֱ�Ϊ8��12���ֽ���20������ĸ߶ȱ�д����ͼ��ʾ��Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���������á���������175cm���£�������175cm������Ϊ�����������á�����ֻ�С�B�������á��IJſ��Գ��ۣ�
ij��ʦ������������ϡ����A��B�������ֱ�Ϊ8��12���ֽ���20������ĸ߶ȱ�д����ͼ��ʾ��Ҷͼ����λ��cm������������175cm���ϣ�����175cm������Ϊ���������á���������175cm���£�������175cm������Ϊ�����������á�����ֻ�С�B�������á��IJſ��Գ��ۣ�| 5 |
| 20 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 7 |
| 10 |
| C | 2 8 |
| 8��7 |
| 2��1 |
| C | 2 3 |
| 3 |
| 28 |


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A����1�� | B����2�� |
| C����3�� | D����4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A��c3+c+1��c2+
| ||||
| B��|a-b|��|a-c|+|b-c| | ||||
C����a+4b=1����
| ||||
| D��ax2+bx+c��0��x��R�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 4 |
| (n-1)an |
| n-an |
| 1 |
| 3an |
| 2 |
| 3 |
| n |
 |
| k=1 |
| 7 |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
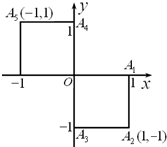 �ס��ҡ���������Ҫѡһ��ȥ�μӳ�����������������ƶ���һ��������Ϊ������ͼ����OΪ��㣬�ٴ�A1��A2��A3��A4��A5����5��������ȡ����ֱ�Ϊ�յ�õ�������������������������������ΪX����X��0���ü�ȥ����X=0������ȥ����X��0���DZ�ȥ��
�ס��ҡ���������Ҫѡһ��ȥ�μӳ�����������������ƶ���һ��������Ϊ������ͼ����OΪ��㣬�ٴ�A1��A2��A3��A4��A5����5��������ȡ����ֱ�Ϊ�յ�õ�������������������������������ΪX����X��0���ü�ȥ����X=0������ȥ����X��0���DZ�ȥ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| m |
| 3 |
| n |
| m |
| n |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 4 |
| 1 |
| 2-an |
| 1 |
| an-1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com