
| 3 |
| 4 |
| 1 |
| 2-an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 |
| 2-an |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 | ||
|
| 1 |
| an-1 |
| 2-an |
| an-1 |
| 1 |
| an-1 |
| 1 |
| a1-1 |
| 1 | ||
|
| 1 |
| an-1 |
| 1 |
| an-1 |
| n+2 |
| n+3 |
| 1 |
| n+3 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| 1 |
| 4 |
| 1 |
| n+4 |
| n |
| 4(n+4) |
| n+2 |
| n+3 |
| 2n |
| n+4 |
| -n2+8 |
| (n+3)(n+4) |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| A、α内的所有直线与m异面 |
| B、α内的直线与m都相交 |
| C、α内存在唯一的直线与m平行 |
| D、α内不存在与m平行的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:
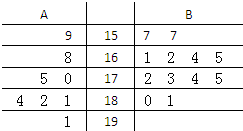 某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为8与12,现将这20株树苗的高度编写成如图所示茎叶图(单位:cm).若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x |
| 1+x |
| 4 |
| 5 |
| 1-x |
| 1+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
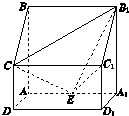 如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图所示,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
| ||
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 态度 调查人群 |
赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com