
【题目】已知函数f(x)=2sin(ωx+φ)(﹣π<φ<0,ω>0)的图象关于直线 ![]() 对称,且两相邻对称中心之间的距离为
对称,且两相邻对称中心之间的距离为 ![]() .
.
(1)求函数y=f(x)的单调递增区间;
(2)若关于x的方程f(x)+log2k=0在区间 ![]() 上总有实数解,求实数k的取值范围.
上总有实数解,求实数k的取值范围.
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,平面PAB⊥平面ABC. (Ⅰ)求直线PC与平面ABC所成角的大小;
(Ⅱ)求二面角B﹣AP﹣C的大小.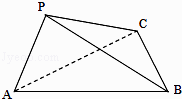
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=loga(a﹣x+1)+bx(a>0,a≠1)是偶函数,则( )
A.b= ![]() 且f(a)>f(
且f(a)>f( ![]() )
)
B.b=﹣ ![]() 且f(a)<f(
且f(a)<f( ![]() )
)
C.b= ![]() 且f(a+
且f(a+ ![]() )>f(
)>f( ![]() )
)
D.b=﹣ ![]() 且f(a+
且f(a+ ![]() )<f(
)<f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() x)
x)
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+cos(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期及单调递增区间;
(2)若x是第二象限角,且f(x﹣ ![]() )=﹣
)=﹣ ![]() cos2x,求cosx﹣sinx的值.
cos2x,求cosx﹣sinx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为 ![]() .
.
(1)求椭圆C的方程;
(2)已知动直线y=k(x+1)与椭圆C相交于A、B两点.
①若线段AB中点的横坐标为﹣ ![]() ,求斜率k的值;
,求斜率k的值;
②若点M(﹣ ![]() ,0),求证:
,0),求证: ![]()
![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.已知命题p和q,若“p∨q”为假命题,则命题p和q中必一真一假
B.命题“?c∈R,方程2x2+y2=c表示椭圆”的否定是“?c∈R,方程2x2+y2=c不表示椭圆”
C.命题“若k<9,则方程“ ![]() +
+ ![]() =1表示双曲线”是假命题
=1表示双曲线”是假命题
D.命题“在△ABC中,若sinA< ![]() ,则A<
,则A< ![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com