已知向量$\overrightarrow{a}$.$\overrightarrow{b}$满足$\overrightarrow{a}$=.$\overrightarrow{b}$=.若(2$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$.则x=1．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

9．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$=（1，-$\sqrt{3}$），$\overrightarrow{b}$=（x，3$\sqrt{3}$），若（2$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$，则x=1．

分析利用向量的坐标运算性质、向量垂直与数量积的关系即可得出．

解答解：2$\overrightarrow{a}$+$\overrightarrow{b}$=（2+x，$\sqrt{3}$），
∵（2$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{a}$，∴（2$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$=2+x-3=0，解得x=1．
故答案为：1．

点评本题考查了向量的坐标运算性质、向量垂直与数量积的关系，考查了推理能力与计算能力，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

19．

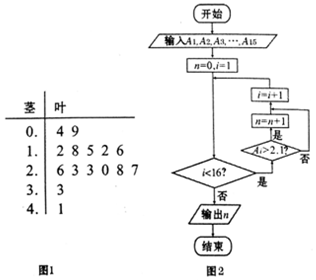图1是随机抽取的15户居民月均用水量（单位：t）的茎叶图，月均用水量依次记为A₁、A₂、…A₁₅，图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图，那么输出的结果n=7．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

20．

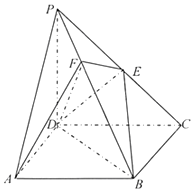《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．
如图，在阳马P-ABCD中，侧棱PD⊥底面ABCD，且PD=CD，E为PC中点，点F在PB上，且PB⊥平面DEF，连接BD，BE．
（Ⅰ）证明：DE⊥平面PBC；
（Ⅱ）试判断四面体DBEF是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；
（Ⅲ）已知AD=2，$CD=\sqrt{2}$，求二面角F-AD-B的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

17．若全集U={1，2，3，4，5，6，7}，集合A={1，3，5，7}，集合B={1，4，7}，则集合（∁_UA）∩B=（　　）

A．

{4}

B．

{1，2，4，6，7}

C．

{3，5}

D．

{1，7}

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

4．已知数列{a_n}的前n项和S_n满足${S_n}={n^2}（{n∈{N^*}}）$，记数列$\left\{{\frac{1}{{{a_n}•{a_{n+1}}}}}\right\}$的前n项和为T_n，则T₂₀₁₇=（　　）

A．

$\frac{4034}{4035}$

B．

$\frac{2017}{4035}$

C．

$\frac{2016}{2017}$

D．

$\frac{2017}{2018}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．

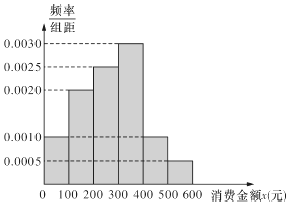长沙梅溪湖步步高购物中心在开业之后，为了解消费者购物金额的分布，在当月的电脑消费小票中随机抽取n张进行统计，将结果分成6组，分别是：[0，100），[100，200），[200，300），[300，400），[400，500），[500，600]，制成如下所示的频率分布直方图（假设消费金额均在[0，600]元的区间内）．
（1）若在消费金额为[400，600]元区间内按分层抽样抽取6张电脑小票，再从中任选2张，求这2张小票均来自[400，500）元区间的概率；
（2）为做好五一劳动节期间的商场促销活动，策划人员设计了两种不同的促销方案．
方案一：全场商品打八折．
方案二：全场购物满100元减20元，满300元减80元，满500元减120元，以上减免只取最高优惠，不重复减免．利用直方图的信息分析：哪种方案优惠力度更大，并说明理由（直方图中每个小组取中间值作为该组数据的替代值）．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

1．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，且|$\overrightarrow{a}$|=2$\sqrt{3}$，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{6}$，$\overrightarrow{a}$⊥（3$\overrightarrow{a}$-$\overrightarrow{b}$），则|$\overrightarrow{b}$|等于（　　）

A．

B．

6$\sqrt{3}$

C．

D．

12$\sqrt{3}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{ax-1}，x≥0}\\{-{x}^{2}-4x，x＜0}\end{array}\right.$，若f（f（-2））=3，则a=$\frac{5}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．在等差数列{a_n}中，a₁+3a₈+a₁₅=60，则2a${\;}_{{9}_{\;}}$-a₁₀的值为（　　）

A．

B．

C．

D．

查看答案和解析>>

同步练习册答案