
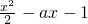 ,(其中a∈R.无理数e=2.71828…)
,(其中a∈R.无理数e=2.71828…) 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
时,求曲线y=f(x)在点(1,f(1))处的切线方程; 时,若关于x的不等式f(x)≥0恒成立,试求a的最大值.
时,若关于x的不等式f(x)≥0恒成立,试求a的最大值. 时,函数f(x)=ex-
时,函数f(x)=ex-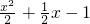 ,求导数可得f′(x)=ex-x+
,求导数可得f′(x)=ex-x+
 ,f(1)=e-1
,f(1)=e-1 )(x-1),即(e-
)(x-1),即(e- )x-y-
)x-y- =0;
=0; x2-1,因为x
x2-1,因为x ,所以a≤
,所以a≤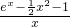 .
.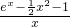 ,则g′(x)=
,则g′(x)=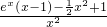 .
. x2+1,所以h′(x)=x(ex-1).
x2+1,所以h′(x)=x(ex-1). ,所以h′(x)>0,所以h(x)在[
,所以h′(x)>0,所以h(x)在[ ,+∞)上单调增
,+∞)上单调增 )=
)= -
-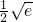 >0
>0 ,+∞)上单调增
,+∞)上单调增 )=2
)=2 -
-
 -
-
 -
- .
.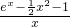 ,确定右边所对应函数的单调性,求出其最小值,即可求得结论.
,确定右边所对应函数的单调性,求出其最小值,即可求得结论.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com