
【题目】设函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)设![]() ≤
≤![]() ,记
,记![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() (
(![]() 为常数),若使
为常数),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的实数
上恒成立的实数![]() 有且只有一个,求实数
有且只有一个,求实数![]() 和
和![]() 的值.
的值.
【答案】(1) 当![]() 时,有极大值
时,有极大值![]()
![]() 极小值
极小值![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() ,
,![]() .
.
【解析】
试题分析:(1)求函数![]() 的导数,由
的导数,由![]() 得
得![]() ,分区间列表讨论函数
,分区间列表讨论函数![]() 的符号与函数
的符号与函数![]() 的单调性,可求函数的极值; (2) 由(1)知
的单调性,可求函数的极值; (2) 由(1)知![]() 区间
区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,分
上单调递减,分![]() 与
与![]() 分别求函数
分别求函数![]() 的最大值
的最大值![]() ,再计算
,再计算![]() 的最小值即可;(3)
的最小值即可;(3)![]() ,构造函数
,构造函数![]() ,求函数
,求函数![]() 的导数,通过导数求函数的最小值,由
的导数,通过导数求函数的最小值,由![]() 得
得![]() ,又
,又![]() ,所以
,所以![]() ,由
,由![]() 的唯一性,可得
的唯一性,可得![]() ,
,![]() .
.
试题解析: (1)![]()
∴当![]() 变化时,可以得到如下表格:
变化时,可以得到如下表格:
|
|
|
|
|
|
|
| 0 | — | 0 |
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
∴当![]() 时,有极大值
时,有极大值![]()
![]() 极小值
极小值![]() ,
,
(2)由(1)知![]() 区间
区间![]() 分别单调增,单调减,单调增,
分别单调增,单调减,单调增,
所以当![]() 时,
时,![]() ,特别当
,特别当![]() 时,有
时,有![]() ;
;
当![]() 时,
时,![]() ,则
,则 ,
,
所以对任意的![]() ,
,![]()
(3)由已知得![]() 在
在![]() 上恒成立,
上恒成立,
则![]()
∴![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
故![]() 时,函数
时,函数![]() 取到最小值.从而
取到最小值.从而![]() ;
;
![]() 在
在![]() 上恒成立,则
上恒成立,则![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
故![]() 时,函数
时,函数![]() 取到最小值.从而
取到最小值.从而![]() ,
,![]()
![]()
由![]() 的唯一性知
的唯一性知![]() ,
,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司采用招考方式引进人才,规定必须在![]() ,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 测试合格的概率分别为
测试合格的概率分别为![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)试证明函数![]() 是偶函数;
是偶函数;
(2)画出![]() 的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
(3)请根据图象指出函数![]() 的单调递增区间与单调递减区间;(不必证明)
的单调递增区间与单调递减区间;(不必证明)
(4)当实数![]() 取不同的值时,讨论关于
取不同的值时,讨论关于![]() 的方程
的方程![]() 的实根的个数;(不必求出方程的解)
的实根的个数;(不必求出方程的解)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扬州瘦西湖隧道长![]() 米,设汽车通过隧道的速度为
米,设汽车通过隧道的速度为![]() 米/秒
米/秒![]() .根据安全和车流的需要,当
.根据安全和车流的需要,当![]() 时,相邻两车之间的安全距离
时,相邻两车之间的安全距离![]() 为
为![]() 米;当
米;当![]() 时,相邻两车之间的安全距离
时,相邻两车之间的安全距离![]() 为
为![]() 米(其中
米(其中![]() 是常数).当
是常数).当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
(1)求![]() 的值;
的值;
(2)一列由![]() 辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为
辆汽车组成的车队匀速通过该隧道(第一辆汽车车身长为![]() 米,其余汽车车身长为
米,其余汽车车身长为![]() 米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第
米,每辆汽车速度均相同).记从第一辆汽车车头进入隧道,至第![]() 辆汽车车尾离开隧道所用的时间为
辆汽车车尾离开隧道所用的时间为![]() 秒.
秒.
①将![]() 表示为
表示为![]() 的函数;
的函数;
②要使车队通过隧道的时间![]() 不超过
不超过![]() 秒,求汽车速度
秒,求汽车速度![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,求cosB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 .(填序号)
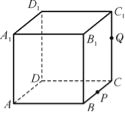
①当0<CQ<![]() 时,S为四边形;
时,S为四边形;
②当CQ=![]() 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=![]() ;
;
④当![]() <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com