
【题目】已知两个函数![]() ,
,![]()
(Ⅰ)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(Ⅱ)求证:对任意![]() ,不等式
,不等式![]() 都成立.
都成立.
【答案】(Ⅰ)分类讨论,详见解析;(Ⅱ)证明见解析.
【解析】
(Ⅰ)利用导数得出![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数,然后分
上为增函数,然后分![]() 和
和![]() 两种情况讨论
两种情况讨论
(Ⅱ)求出![]() 的最小值和
的最小值和![]() 的最大值,将问题转化为两函数最值之间大小关系的判断即可.
的最大值,将问题转化为两函数最值之间大小关系的判断即可.
(Ⅰ)由![]() 得:
得:![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
∴![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数
上为增函数
①当![]() 时,
时,![]() 在区间
在区间![]() 上为增函数,
上为增函数,
![]() 的最大值为
的最大值为![]()
②当![]() 时,
时,![]()
![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数
上为增函数
∴![]() 的最大值为
的最大值为![]()
下面比较![]() 与
与![]() 大小
大小

∵![]()
∴当![]() 时,
时,![]() ,
,
故![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]()
当![]() 时,
时,![]() ,
,
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]()
综上可知:当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]()
当![]() 时,
时,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]()
(Ⅱ)证明:由(Ⅰ)知,当![]() 时,
时,![]() 在区间
在区间![]() 上为减函数,在区间
上为减函数,在区间![]() 上为增函数
上为增函数
所以当![]() 时,
时,![]()
又由![]() 得:
得:![]()
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
∴![]() 在区间
在区间![]() 上为增函数,在区间
上为增函数,在区间![]() 上为减函数
上为减函数
所以当![]() 时,
时,![]()
综上可知,当![]() 时,不等式
时,不等式![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】双纽线最早于1694年被瑞士数学家雅各布·伯努利用来描述他所发现的曲线.在平面直角坐标系![]() 中,把到定点
中,把到定点![]() ,
,![]() 距离之积等于
距离之积等于![]() 的点的轨迹称为双纽线
的点的轨迹称为双纽线![]() .已知点
.已知点![]() 是双纽线
是双纽线![]() 上一点,下列说法中正确的有( )
上一点,下列说法中正确的有( )
①双纽线经过原点![]() ; ②双纽线
; ②双纽线![]() 关于原点
关于原点![]() 中心对称;
中心对称;
③![]() ; ④双纽线
; ④双纽线![]() 上满足
上满足![]() 的点
的点![]() 有两个.
有两个.
A.①②B.①②③C.②③D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为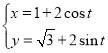 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求![]() ;
;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() :
:![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() ,且
,且![]() 的面积不超过
的面积不超过![]() ,求直线
,求直线![]() 的倾斜角的取值范围.
的倾斜角的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.对具有线性相关关系的变量![]() 有一组观测数据
有一组观测数据![]() ,其线性回归方程是
,其线性回归方程是![]() ,且
,且![]() ,则实数
,则实数![]() 的值是
的值是![]()
B.正态分布![]() 在区间
在区间![]() 和
和![]() 上取值的概率相等
上取值的概率相等
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
D.若一组数据![]() 的平均数是2,则这组数据的众数和中位数都是2
的平均数是2,则这组数据的众数和中位数都是2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点
),在极坐标系(与平面直角坐标系取相同的单位长度,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() 可,试判断曲线
可,试判断曲线![]() 和
和![]() 的位置关系;
的位置关系;
(2)若曲线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 两点,且
两点,且![]() ,满足
,满足![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当a=-2时,求函数f(x)的极值;
(2)若ln[e(x+1)]≥2- f(-x)对任意的x∈[0,+∞)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:
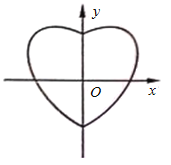
①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
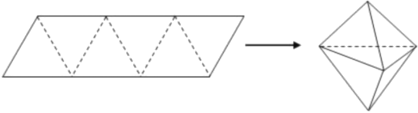
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽粒,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为2的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的表面积为________;该六面体内有一球,则该球体积的最大值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com