
分析 (1)由数列{an}的定义,可得前11项,进而得到前11项和,再由定义集合Pl,即可得到元素个数;
(2)运用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).再结合定义,运用等差数列的求和公式,即可得到所求.
解答 解:(1)由数列{an}的定义得a1=1,a2=-2,a3=-2,a4=3,
a5=3,a6=3,a7=-4,a8=-4,a9=-4,a10=-4,a11=5,
所以S1=1,S2=-1,S3=-3,S4=0,S5=3,S6=6,S7=2,
S8=-2,S9=-6,S10=-10,S11=-5,
从而S1=a1,S4=0•a4,S5=a5,S6=2a6,S11=-a11,
所以集合P11中元素的个数为5;
(2)先证:Si(2i+1)=-i(2i+1)(i∈N*).
事实上,①当i=1时,Si(2i+1)=S3=-3,-i(2i+1)=-3,故原等式成立;
②假设i=m时成立,即Sm(2m+1)=-m(2m+1),则i=m+1时,
S(m+1)(2m+3)=Sm(2m+1)+(2m+1)2-(2m+2)2=-m(2m+1)-4m-3
=-(2m2+5m+3)=-(m+1)(2m+3).
综合①②可得Si(2i+1)=-i(2i+1).于是S(i+1)(2i+1)=Si(2i+1)+(2i+1)2
=-i(2i+1)+(2i+1)2=(2i+1)(i+1).
由上可知Si(2i+1)是2i+1的倍数,而ai(2i+1)+j=2i+1(j=1,2,…,2i+1),
所以Si(2i+1)+j=Si(2i+1)+j(2i+1)是ai(2i+1)+j(j=1,2,…,2i+1)的倍数.
又S(i+1)(2i+1)=(i+1)•(2i+1)不是2i+2的倍数,
而a(i+1)(2i+1)+j=-(2i+2)(j=1,2,…,2i+2),
所以S(i+1)(2i+1)+j=S(i+1)(2i+1)-j(2i+2)=(2i+1)(i+1)-j(2i+2)
不是a(i+1)(2i+1)+j(j=1,2,…,2i+2)的倍数,
故当l=i(2i+1)时,集合Pl中元素的个数为1+3+…+(2i-1)=i2,
于是,当l=i(2i+1)+j(1≤j≤2i+1)时,集合Pl中元素的个数为i2+j.
又2000=31×(2×31+1)+47,
故集合P2 000中元素的个数为312+47=1008.
点评 本题考查集合、数列的概念和运算、计数原理等基础知识,考查探究能力,以及运用数学归纳法的推理论证能力,有一定的难度.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{3}{5}$,-$\frac{4}{5}$) | B. | (-$\frac{3}{5}$,$\frac{4}{5}$) | C. | ($\frac{3}{5}$,-$\frac{4}{5}$)或(-$\frac{3}{5}$,$\frac{4}{5}$) | D. | ($\frac{4}{5}$,-$\frac{3}{5}$)或(-$\frac{4}{5}$,$\frac{3}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
若数列的前4项为1,0,1,0,则这个数列的通项公式不可能是( )
A.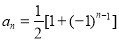
B.
C.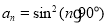
D.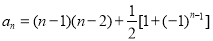
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:选择题
某几何体三视图如图所示,则该几何体的体积为(俯视图中弧线是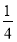 圆弧)( )
圆弧)( )

A. B.
B.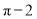
C.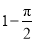 D.
D.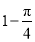
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com