
分析 用辅助角法将原函数转化为y=$\sqrt{13}$sin(φ-x)(其中tanφ=$\frac{2}{3}$).再应用整体思想求解.
解答 解:y=2cosx-3sinx=$\sqrt{13}$sin(φ-x)(其中tanφ=$\frac{2}{3}$).
y有最大值时,应sin(φ-x)=1⇒φ-x=2kπ+$\frac{π}{2}$⇒-x=2kπ+$\frac{π}{2}$-φ.
∴tanx=-tan(-x)=-tan(2kπ+$\frac{π}{2}$-φ)=-cotφ=-$\frac{1}{tanφ}$=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题主要考查在三角函数中用辅助角法将一般的函数转化为一个角的一种三角函数,用整体思想来应用三角函数的性质解题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(理)试卷(解析版) 题型:解答题
已知抛物线 :
: (
(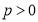 )与椭圆
)与椭圆 :
: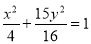 相交所得的弦长为
相交所得的弦长为
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)设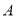 ,
,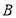 是
是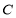 上异于原点
上异于原点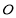 的两个不同点,直线
的两个不同点,直线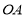 和
和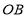 的倾斜角分别为
的倾斜角分别为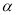 和
和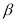 ,当
,当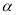 ,
,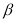 变化且
变化且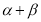 为定值
为定值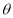 (
(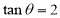 )时,证明:直线
)时,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com