Question

14．已知f（x）=x²+2x+1-sin$\frac{a-b}{3}$π
（Ⅰ）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求函数f（x）有零点的概率
（Ⅱ）若a是从区间[0，3]中任取的一个数，b是从区间[0，2]中任取的一个数，求函数f（x）有零点的概率．

Answer 1

分析 （Ⅰ）问题等价于sin$\frac{a-b}{3}$π≥0，列举可得基本事件共有15个，事件A包含6个基本事件，可得概率；
（Ⅱ）作出图形，由几何概型的概率公式可得．

解答 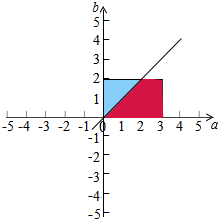解：（Ⅰ）函数f（x）=x²+2x+1-sin$\frac{a-b}{3}$π有零点等价于方程x²+2x+1-sin$\frac{a-b}{3}$π=0有实根，
∵x²+2x+1≥0，∴sin$\frac{a-b}{3}$π≥0
记事件A为函数f（x）=x²+2x+1-sin$\frac{a-b}{3}$π有零点，
总的基本事件共有12个：（0，0），（0，1），（0，2），（1，0），
（1，1），（1，2），（2，0），（2，1），（2，2），（3，0），（3，1），
（3，2），事件A包含9个基本事件：（0，0），（1，0），（1，1），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2），9个．
∴P（A）=$\frac{9}{12}$=$\frac{3}{4}$
（Ⅱ）如图，试验的全部结果所构成的区域为（矩形区域）a是从区间[0，3]中任取的一个数，b是从区间[0，2]中任取的一个数，
函数表示事件A，所构成的区域为A={（a，b）|sin$\frac{a-b}{3}$π≥0且（a，b）∈Ω}即图中的阴影部分．
∴P（A）=$1-\frac{\frac{1}{2}×2×2}{2×3}$=$\frac{2}{3}$．

点评 本题考查古典概型和几何概型，关键是首先明确概率模型，然后根据根式解答；属中档题．