
求由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形面积.
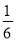
【解析】(1)化整为零,插入等分点.
将曲边梯形分成n个小曲边梯形,用分点
 ,
,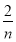 ,…,
,…,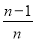 把区间[0,1]等分成n个小区间
把区间[0,1]等分成n个小区间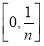 ,
,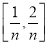 ,…,
,…,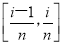 ,…,
,…,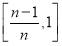 .简写作:
.简写作: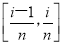 (i=1,2,…,n).
(i=1,2,…,n).
每个小区间的长度为Δx=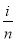 -
-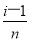 =
= .
.
过各分点作x轴的垂线,把曲边梯形分成n个小曲边梯形,它们的面积分别记作:
ΔS1,ΔS2,…,ΔSi,…,ΔSn.
(2)以直代曲,估计误差.
用小矩形面积近似代替小曲边梯形面积.
在小区间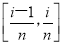 上任取一点xi(i=1,2,…,n),
上任取一点xi(i=1,2,…,n),
为了计算方便,取xi为小区间的左端点,用xi对应的函数值f(xi)=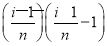 为一边,以小区间长度Δx=
为一边,以小区间长度Δx=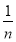 为邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为:ΔSi≈f(xi)·Δx=
为邻边的小矩形面积近似代替第i个小曲边梯形面积,可以近似地表示为:ΔSi≈f(xi)·Δx=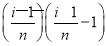 ·
·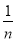 (i=1,2,…,n).
(i=1,2,…,n).
(3)积零成整,精益求精.
因为每一个小矩形的面积都可以作为相应的小曲边梯形面积的近似值,所以n个小矩形面积的和,就是曲边梯形面积S的近似值.即:
S=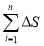 i≈
i≈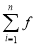 (xi)Δx=
(xi)Δx=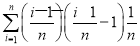 =-
=-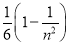 .①
.①
当分点数目越多,即Δx越小时,和式①的值就越接近曲边梯形的面积S.因此,当n趋于+∞时,即Δx趋于0时,和式①的极限值就是所求曲边梯形的面积.
Δx趋于0时,S趋于-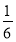 (负号表示图象在x轴下方).所以,由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形的面积是
(负号表示图象在x轴下方).所以,由直线x=0,x=1,y=0和曲线y=x(x-1)围成的图形的面积是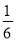 .
.


科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4章末练习卷(解析版) 题型:解答题
设函数f(x)=a2ln x-x2+ax,a>0.
①求f(x)的单调区间;②求所有实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4.5练习卷(解析版) 题型:选择题
由曲线y=x3,直线x=0,x=1及y=0所围成的曲边梯形的面积为( ).
A.1 B.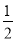 C.
C.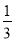 D.
D. 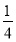
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4.4练习卷(解析版) 题型:解答题
请你设计一个包装盒,如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E,F在AB上,是被切去的一个等腰直角三角形,斜边的两个端点,设AE=FB=x(cm).
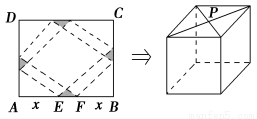
①某广告商要求包装盒的侧面积S(cm2)最大,试问x应取何值?
②某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4.3练习卷(解析版) 题型:解答题
已知f(x)=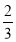 x+
x+ ,h(x)=
,h(x)=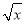 ,设F(x)=f(x)-h(x),求F(x)的单调区间与极值.
,设F(x)=f(x)-h(x),求F(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源:2015届湘教版高二数学选修2-2基础达标4.1练习卷(解析版) 题型:填空题
若曲线y=x2+ax+b在点(0,b)处的切线方程为x-y+1=0,则a,b的值分别为________,________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com