已知函数f(x)=x3+ax2+bx+c(a,b,c∈R),当且仅当x=1,x=-1 时,f(x)取得极值,并且极大值比极小值大c.
(1)求常数a,b,c的值;
(2)求f(x)的极值.
解:(1)因为f'(x)=3x
2+2ax+b;
∵当x=-1和x=1时,f(x)取得极值,
∴f′(-1)=0,f′(1)=0,
∴
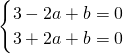
?
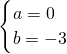
.
∴f′(x)=3(x
2-1)=3(x+1)(x-1).
∴当x>1或x<-1时,f′(x)>0;原函数递增;
当-1<x<1时,f′(x)<0函数递减.
∴函数极大值为:f(-1)=-1-b+c,极小值为:f(1)=1+b+c
∴(-1-b+c)-(1+b+c)=c?c=4.
(2)∵f(x)=x
3-3x+4.
∴函数极大值为f(-1)=6;极小值为:f(1)=2.
分析:(1)求出f(x)的导函数,令导函数在两个极值点处的值为0,列出方程组,求出a,b的值;再结合极大值比极小值大c即可求出c的值;
(2)直接根据第一问中求出的结论代入即可.
点评:求函数的极值,一般求出函数的导数,求出导函数大于0的x范围及导函数小于0的x的范围,列出x,f′(x),f(x0的情况变化表从而得到函数的极值;注意函数在极值点处的导数值为0.

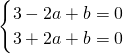 ?
?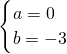 .
.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<