[题目]已知命题函数在上是减函数.命题 .．(1)若为假命题.求实数的取值范围,(2)若“或为假命题.求实数的取值范围．题目和参考答案——青夏教育精英家教网—

【题目】已知命题函数在上是减函数，命题，．

（1）若为假命题，求实数的取值范围；

（2）若“或”为假命题，求实数的取值范围．

【答案】（1）；（2）

【解析】分析：第一问利用命题的否定和命题本身是一真一假的，根据命题q是假命题，得到命题的否定是真命题，结合二次函数图像，得到相应的参数的取值范围；第二问利用“或”为假命题，则有两个命题都是假命题，所以先求命题p为真命题时参数的范围，之后求其补集，得到m的范围，之后将两个命题都假时参数的范围取交集，求得结果.

详解：（1）因为命题，

所以：，，

当为假命题时，等价于为真命题，

即在上恒成立，

故，解得

所以为假命题时，实数的取值范围为.

（2）函数的对称轴方程为，

当函数在上是减函数时，则有

即为真时，实数的取值范围为

“或”为假命题，故与同时为假，

则，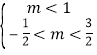

综上可知，当 “或”为假命题时，实数的取值范围为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】设抛物线的顶点在坐标原点，焦点F在轴正半轴上，过点F的直线交抛物线于A,B两点，线段AB的长是8，AB的中点到轴的距离是．

(1)求抛物线的标准方程；

(2)在抛物线上是否存在不与原点重合的点P，使得过点P的直线交抛物线于另一点Q，满足，且直线PQ与抛物线在点P处的切线垂直？并请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂为了安排生产任务，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

零件的个数x（件）
加工的时间y（小时）

（1）在给定的坐标系中画出表中数据的散点图；

（2）求出y关于x的线性回归方程，并在坐标系中画出回归直线；

（3）试预测生产10个零件需要多少时间.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图.

(1)求分数在的频数及全班人数；

(2)求分数在之间的频数，并计算频率分布直方图中间矩形的高.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某公司为招聘新员工设计了一个面试方案:应聘者从道备选题中一次性随机抽取道题，按照题目要求独立完成规定:至少正确完成其中道题的便可通过.已知道备选题中应聘者甲有道题能正确完成，道题不能完成；应聘者乙每题正确完成的概率都是，且每题正确完成与否互不影响

（1)分别求甲、乙两人正确完成面试题数的分布列，并计算其数学期望；

（2）请分析比较甲、乙两人谁的面试通过的可能性大？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数.

(1)求函数的单调区间;

(2)当时,函数的图象恒不在轴的上方,求实数的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】甲乙两支排球队进行比赛，先胜3局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是，其余每局比赛甲队获胜的概率都是．设各局比赛结果相互独立．
（1）分别求甲队3：0，3：1，3：2胜利的概率；
（2）若比赛结果3：0或3：1，则胜利方得3分，对方得0分；若比赛结果为3：2，则胜利方得2分，对方得1分，求乙队得分X的分布列及数学期望．