
已知函数 定义在R上.
定义在R上.
(1)若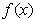 可以表示为一个偶函数
可以表示为一个偶函数 与一个奇函数
与一个奇函数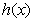 之和,设
之和,设 ,
,
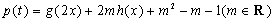 ,求出
,求出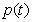 的解析式;
的解析式;
(2)若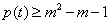 对于
对于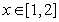 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(3)若方程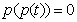 无实根,求m的取值范围.
无实根,求m的取值范围.
解:(1)假设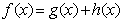 ①,其中
①,其中 偶函数,
偶函数,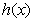 为奇函数,
为奇函数,
则有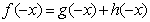 ,即
,即 ②,
②,
由①②解得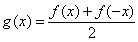 ,
,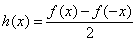 .
.
∵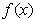 定义在R上,∴
定义在R上,∴ ,
,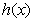 都定义在R上.
都定义在R上.
∵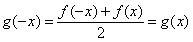 ,
,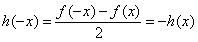 .
.
∴ 是偶函数,
是偶函数,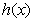 是奇函数,∵
是奇函数,∵ ,
,
∴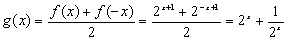 ,
,
 . 由
. 由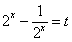 ,则
,则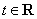 ,
,
平方得 ,∴
,∴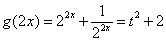 ,
,
∴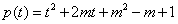 . ………………………………6分
. ………………………………6分
(2)∵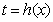 关于
关于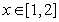 单调递增,∴
单调递增,∴ .
.
∴ 对于
对于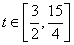 恒成立,
恒成立,
∴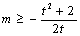 对于
对于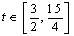 恒成立,令
恒成立,令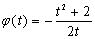 ,则
,则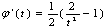 ,
,
∵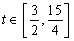 ,∴
,∴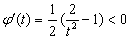 ,故
,故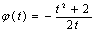 在
在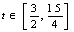 上单调递减,
上单调递减,
∴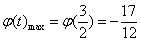 ,∴
,∴ 为m的取值范围. 11分
为m的取值范围. 11分
(3)由(1)得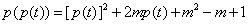 ,
,
若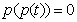 无实根,即
无实根,即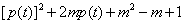 ①无实根,
①无实根,
方程①的判别式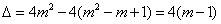 .
.
1°当方程①的判别式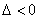 ,即
,即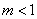 时,方程①无实根.
时,方程①无实根.
2°当方程①的判别式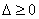 ,即
,即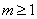 时,
时,
方程①有两个实根 ,
,
即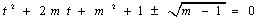 ②,
②,
只要方程②无实根,故其判别式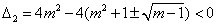 ,
,
即得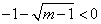 ③,且
③,且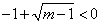 ④,
④,
∵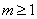 ,③恒成立,由④解得
,③恒成立,由④解得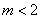 , ∴③④同时成立得
, ∴③④同时成立得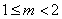 .
.
综上,m的取值范围为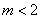 .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com