
(09年泗阳中学模拟六)(14分)
已知函数f(x)=![]() 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为![]()
(Ⅰ)求f(![]() )的值;
)的值;
(Ⅱ)将函数y=f(x)的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
解析:(Ⅰ)f(x)=![]()
=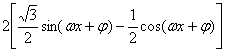
=2sin(![]() -
-![]() )
)
因为 f(x)为偶函数,
所以 对x∈R,f(-x)=f(x)恒成立,
因此 sin(-![]() -
-![]() )=sin(
)=sin(![]() -
-![]() ).
).
即-sin![]() cos(
cos(![]() -
-![]() )+cos
)+cos![]() sin(
sin(![]() -
-![]() )=sin
)=sin![]() cos(
cos(![]() -
-![]() )+cos
)+cos![]() sin(
sin(![]() -
-![]() ),
),
整理得 sin![]() cos(
cos(![]() -
-![]() )=0.因为
)=0.因为 ![]() >0,且x∈R,所以 cos(
>0,且x∈R,所以 cos(![]() -
-![]() )=0.
)=0.
又因为 0<![]() <π,故
<π,故 ![]() -
-![]() =
=![]() .所以 f(x)=2sin(
.所以 f(x)=2sin(![]() +
+![]() )=2cos
)=2cos![]() .
.
由题意得 ![]()
故 f(x)=2cos2x.
因为 ![]()
(Ⅱ)将f(x)的图象向右平移个![]() 个单位后,得到
个单位后,得到![]() 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到
的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到![]() 的图象.
的图象.
![]()
当 2kπ≤![]() ≤2 kπ+ π (k∈Z),
≤2 kπ+ π (k∈Z),
即 4kπ+≤![]() ≤x≤4kπ+
≤x≤4kπ+![]() (k∈Z)时,g(x)单调递减.
(k∈Z)时,g(x)单调递减.
因此g(x)的单调递减区间为 ![]() (k∈Z)
(k∈Z)


科目:高中数学 来源: 题型:
(09年泗阳中学模拟六)(15分)已知m∈R,直线l:![]() 和圆C:
和圆C:![]() 。
。
(1)求直线l斜率的取值范围;
(2)直线l能否将圆C分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年泗阳中学模拟六)(15分
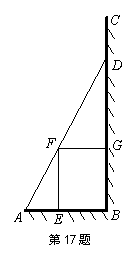
如图,某小区准备在一直角围墙![]() 内的空地上植造一块“绿地
内的空地上植造一块“绿地![]() ”,其中
”,其中![]() 长为定值
长为定值![]() ,
,![]() 长可根据需要进行调节(
长可根据需要进行调节(![]() 足够长).现规划在
足够长).现规划在![]() 的内接正方形
的内接正方形![]() 内种花,其余地方种草,且把种草的面积
内种花,其余地方种草,且把种草的面积![]() 与种花的面积
与种花的面积![]() 的比值
的比值![]() 称为“草花比
称为“草花比![]() ”.
”.
(Ⅰ)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(Ⅱ)当![]() 为多长时,
为多长时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年泗阳中学模拟六)(14分) 如图,在多面体ABCDE中,AE⊥ABC,BD∥AE,
且AC=AB=BC=BD=2,AE=1,F在CD上(不含C, D两点)
(1)求多面体ABCDE的体积;
(2)若F为CD中点,求证:EF⊥面BCD;
(3)当![]() 的值= 时,能使AC ∥平面EFB,并给出证明。
的值= 时,能使AC ∥平面EFB,并给出证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com