
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)若![]() 时都有
时都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
(2)![]()
【解析】
(1)由极值点可知![]() ,从而求得
,从而求得![]() ;根据导函数的正负即可确定
;根据导函数的正负即可确定![]() 的单调区间;
的单调区间;
(2)求导后得到导函数;当![]() 和
和![]() 时,可根据导函数正负确定
时,可根据导函数正负确定![]() 单调递增,从而
单调递增,从而![]() ,满足题意;当
,满足题意;当![]() 时,由零点存在定理可知存在
时,由零点存在定理可知存在![]() ,使得
,使得![]() 时,
时,![]() ,由单调性可知
,由单调性可知![]() 不恒成立;从而得到所求范围.
不恒成立;从而得到所求范围.
(1)由![]() 得:
得:![]() 定义域为
定义域为![]() ,
,![]()
![]() 是
是![]() 的极值点
的极值点 ![]() ,解得:
,解得:![]()
此时![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
(2)![]() ,
,![]()
①当![]() 时,
时,![]() 恒成立
恒成立 ![]() 单调递增
单调递增 ![]() ,满足题意
,满足题意
②当![]() 时,
时,![]() 是
是![]() 上的增函数,且
上的增函数,且![]()
若![]() ,即
,即![]() ,则
,则![]() 且不恒等于
且不恒等于![]()
![]() 单调递增
单调递增 ![]() ,满足题意
,满足题意
若![]() ,即
,即![]() ,
,![]() ,
,![]()
![]() 存在
存在![]() ,使得
,使得![]()
当![]() 时,
时,![]() ,则
,则![]() 单调递减
单调递减 ![]()
即![]() 不恒成立,不合题意
不恒成立,不合题意
综上所述:实数![]() 的取值范围为
的取值范围为![]()


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】已知圆C1的圆心在坐标原点O,且恰好与直线![]() 相切.
相切.
(Ⅰ)求圆C1的标准方程;
(Ⅱ)设点A为圆上一动点,AN垂直于x轴于点N,若动点Q满足![]()
(其中m为非零常数),试求动点Q的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当m=![]() 时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
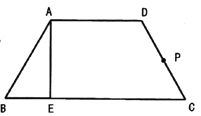
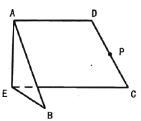
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() 为
为![]() 的中点.沿
的中点.沿![]() 将梯形折成大小为
将梯形折成大小为![]() 的二面角
的二面角![]() ,若
,若![]() 内(含边界)存在一点
内(含边界)存在一点![]() ,使得
,使得![]() 平面
平面![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 交于点P.
交于点P.
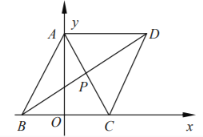
(1)求直线![]() 的方程;
的方程;
(2)若点E,F分别在平行四边形![]() 的边
的边![]() 和
和![]() 上运动,且
上运动,且![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)试写出三角形![]() 区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使
区域(包括边界)所满足的线性约束条件,若在该区域上任取一点M,使![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com