
【题目】若数列![]() 、
、![]() 满足
满足![]() (
(![]() N*),则称
N*),则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() ,若
,若![]() 对任意
对任意![]() 恒成立,求实数M的最小值.
恒成立,求实数M的最小值.
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1){an}不一定为等差数列,如![]() ;
;
(2)设数列{an}的公比为q,解方程可得首项和公比,由等比数列的通项公式和求和公式,计算可得所求值;
(3)由累加法可得数列{an}的通项公式,讨论n为奇数或偶数,求得极限,由不等式恒成立思想可得M的最小值.
解:(1) 如![]() ,则
,则![]() 为常数列,但
为常数列,但![]() 不是等差数列,
不是等差数列,
(2) 设数列![]() 的公比为
的公比为![]() ,则由题意,
,则由题意,![]() 、
、![]() 均为正整数,
均为正整数,
因为![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() ,
,
故![]() 或
或![]() (
(![]() N*),
N*),
①当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
② 当![]() 时,
时,![]() ,
,![]() ,
,![]()
综上,![]() 的值为
的值为![]() 或
或![]() ;
;
(3) 由![]() ≤
≤![]() 且
且![]() ≤
≤![]() 得,
得,![]() =
=![]()
故有:![]() ,
,
![]() ,
,
![]() ,
,
累加得: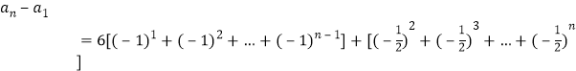
=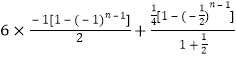
=![]() ,
,
又![]() ,所以
,所以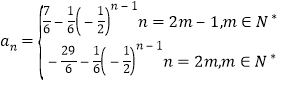
当n为奇数时,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
当n为偶数时,![]() 单调递减,
单调递减,![]() ,
,![]() ,
,
从而![]() ≤
≤![]() ,所以M≥
,所以M≥![]() ,即M的最小值为
,即M的最小值为![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=ax在区间(﹣∞,+∞)上为增函数”的充分不必要条件
C.命题“x∈R,使得x2+x+1<0”的否定是:“x∈R,均有x2+x+1≥0”
D.“若f ′(![]() )=0,则
)=0,则![]() 为y=f(x)的极值点”为真命题
为y=f(x)的极值点”为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,
的中点,![]() .沿
.沿![]() 将△
将△![]() 翻折到△
翻折到△![]() ,连接
,连接![]() ,得到如图的五棱锥
,得到如图的五棱锥![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为8的菱形![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且二面角
的位置,且二面角![]() 为
为![]() .
.
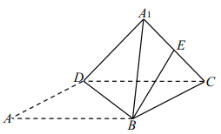
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若点![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一动点(异于点
上一动点(异于点![]() ),
),![]() 为线段
为线段![]() 上一动点,且
上一动点,且![]() .
.
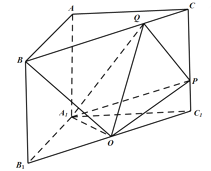
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com