已知双曲线
的一个焦点与抛物线
的焦点重合，且双曲线的离心率等于
，则该双曲线的方程为（ ）
A.
B.
C.
D.
名校课堂系列答案科目：高中数学 来源：2015届山西省高二3月月考文科数学试卷（解析版） 题型：解答题
从某居民区随机抽取10个家庭,获得第
个家庭的月收入
(单位:千元)与月储蓄
(单位:千元)的数据资料,算得
,
,
,
.
(1)求家庭的月储蓄
对月收入
的线性回归方程
;
(2)判断变量
与
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中
,
为样本平均值,线性回归方程也可写为
附:线性回归方程中,
,
,
查看答案和解析>>
科目：高中数学 来源：2015届山东省高二暑假作业数学试卷五（解析版） 题型：解答题
设椭圆C：
(a>b>0)的离心率为
，过原点O斜率为1的直线与椭圆C相交于M，N两点，椭圆右焦点F到直线l的距离为
.
(1)求椭圆C的方程；
(2)设P是椭圆上异于M，N外的一点，当直线PM，PN的斜率存在且不为零时，记直线PM的斜率为k1，直线PN的斜率为k2，试探究k1·k2是否为定值？若是，求出定值；若不是，说明理由．
查看答案和解析>>
科目：高中数学 来源：2015届山东省高二暑假作业数学试卷三（解析版） 题型：解答题
已知数列
是等差数列，
（
）.
（Ⅰ）判断数列
是否是等差数列，并说明理由；
（Ⅱ）如果
，
（
为常数），试写出数列的通项公式；
（Ⅲ）在（Ⅱ）的条件下，若数列得前
项和为
，问是否存在这样的实数
，使当且仅当
时取得最大值.若存在，求出
的取值范围；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源：2015届山东省高二暑假作业数学试卷三（解析版） 题型：选择题
函数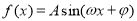
（其中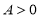
，
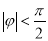）的图象如图所示，为了得到
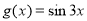的图象，只需将
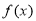的图象（ ）
A.向右平移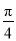
个单位长度 B.向左平移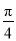个单位长度
C.向右平移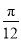
个单位长度 D.向左平移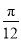个单位长度
查看答案和解析>>
科目：高中数学 来源：2015届山东省高二暑假作业四数学试卷（解析版） 题型：解答题
己知等比数列
所有项均为正数，首
，且
成等差数列．
(I)求数列的通项公式；
(II)数列
的前n项和为
，若
，求实数
的值．
查看答案和解析>>
科目：高中数学 来源：2015届山东省高二暑假作业四数学试卷（解析版） 题型：选择题
给定两个命题p、q，若﹁p是q的必要而不充分条件，则p是﹁q的
A.充分而不必条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目：高中数学 来源：2015届山东省菏泽市高二下学期期末考试文科数学试卷（解析版） 题型：填空题
由下列事实：
（a﹣b）（a+b）=a2﹣b2
（a﹣b）（a2+ab+b2）=a3﹣b3，
（a﹣b）（a3+a2b+ab2+b3）=a4﹣b4，
（a﹣b）（a4+a3b+a2b2+ab3+b4）=a5﹣b5，
可得到合理的猜想是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的焦点为
，得双曲线的
，双曲线的离心率等于
，所以
，进而
，因此双曲线的方程为
，故选择D.
，则
B.
C.
D.