Question

设椭圆C： (a>b>0)的离心率为，过原点O斜率为1的直线与椭圆C相交于M，N两点，椭圆右焦点F到直线l的距离为.

(1)求椭圆C的方程；

(2)设P是椭圆上异于M，N外的一点，当直线PM，PN的斜率存在且不为零时，记直线PM的斜率为k1，直线PN的斜率为k2，试探究k1·k2是否为定值？若是，求出定值；若不是，说明理由．

 

Answer 1

(1)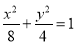；(2) k1·k2是为定值－.

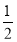【解析】

试题分析：(1)由椭圆C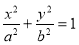： (a>b>0)的离心率为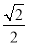可得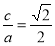,又由椭圆右焦点F(c,0)到直线l的距离为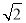,由点到直线的距离公式得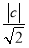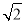＝，从而求得c的值，代入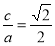求得a的值；再注意到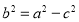从而求得b的值,因此就可写出所求椭圆C的方程; (2)由过原点O斜率为1的直线方程为：y=x，联立椭圆C与直线L的方程就可求出M，N两点的坐标，再由过两点的直线的斜率公式就可用点P的坐标表示出kPM·kPN，再注意点P的坐标满足椭圆C的方程，从而就可求出k1·k2＝kPM·kPN是否与点P的坐标有关，若与点P的坐标无关则k1·k2的值为定值；否则不为定值．

试题解析：(1)设椭圆的焦距为2c(c>0)，焦点F(c,0)，直线l：x－y＝0，

F到l的距离为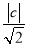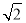＝，解得c＝2，

又∵e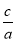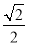＝＝，∴a＝2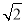，∴b＝2.

∴椭圆C的方程为.

(2)由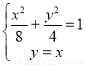解得x＝y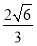＝，或x＝y＝－，

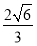不妨设M，N，P(x，y)，

∴kPM·kPN＝

由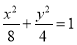，即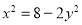，代入化简得k1·k2＝kPM·kPN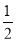＝－为定值．

考点：１．椭圆的标准方程；２．直线与椭圆的位置关系．