
若x,y满足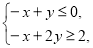 则
则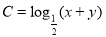 的最大值为 .
的最大值为 .
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源:2015届山西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
对任意复数 、
、 ,定义
,定义 ,其中
,其中 是
是 的共轭复数.对任意复数
的共轭复数.对任意复数 、
、 、
、 ,有如下四个命题:
,有如下四个命题:
① ;
;
② ;
;
③ ;
;
④ .
.
则真命题的个数是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山西大学附中高二第二学期月考理科数学试卷(解析版) 题型:选择题
设 为曲线
为曲线 :
: 上的点,且曲线
上的点,且曲线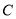 在点
在点 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为 ,则点
,则点 横坐标的取值范围为
横坐标的取值范围为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业数学试卷五(解析版) 题型:解答题
设椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为
,过原点O斜率为1的直线与椭圆C相交于M,N两点,椭圆右焦点F到直线l的距离为 .
.
(1)求椭圆C的方程;
(2)设P是椭圆上异于M,N外的一点,当直线PM,PN的斜率存在且不为零时,记直线PM的斜率为k1,直线PN的斜率为k2,试探究k1·k2是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业数学试卷五(解析版) 题型:选择题
设a、b、c均为正实数,则三个数a+ 、b+
、b+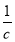 、c+
、c+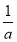 ( ).
( ).
A.都大于2 B.都小于2
C.至少有一个不大于2 D.至少有一个不小于2
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业数学试卷三(解析版) 题型:解答题
已知数列 是等差数列,
是等差数列, (
( ).
).
(Ⅰ)判断数列 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(Ⅱ)如果 ,
, (
( 为常数),试写出数列
为常数),试写出数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,若数列 得前
得前 项和为
项和为 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使 当且仅当
当且仅当 时取得最大值.若存在,求出
时取得最大值.若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业四数学试卷(解析版) 题型:解答题
己知等比数列 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列.
(I)求数列 的通项公式;
的通项公式;
(II)数列 的前n项和为
的前n项和为 ,若
,若 ,求实数
,求实数 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届山东省菏泽市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
有一段“三段论”推理是这样的:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点;因为函数f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.”以上推理中
(1)大前提错误;(2)小前提错误;(3)推理形式正确;(4)结论正确
你认为正确的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com