
分析 (1)利用两个向量的数量积的定义,根据|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(2\overrightarrow{a}-\overrightarrow{b})}^{2}}$,求得它的值.
(2)利用同角三角函数的基本关系,求得要求式子的值.
解答 解:(1)因为|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为60°,
所以$|2\overrightarrow a-\overrightarrow b|=\sqrt{4{{\overrightarrow a}^2}-4\overrightarrow a•\overrightarrow b+{{\overrightarrow b}^2}}=\sqrt{4×{2^2}-4×2×1×cos60°+{1^2}}=\sqrt{13}$.
(2)$\frac{{5{{sin}^3}θ+cosθ}}{{2{{cos}^3}θ+{{sin}^2}θcosθ}}=\frac{{5{{sin}^3}θ+cosθ({{sin}^2}θ+{{cos}^2}θ)}}{{2{{cos}^3}θ+{{sin}^2}θcosθ}}$=$\frac{{5sin}^{3}θ{+sin}^{2}θcosθ{+cos}^{3}θ}{{2cos}^{3}θ{+sin}^{2}θcosθ}$=$\frac{{5{{tan}^3}θ+{{tan}^2}θ+1}}{{2+{{tan}^2}θ}}$=$\frac{{5×{3^3}+{3^2}+1}}{{2+{3^2}}}=\frac{145}{11}$.
点评 本题主要考查两个向量的数量积的定义,同角三角函数的基本关系,属于基础题.


科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=-1,c=1,d=0.1,则输出的x的值为( )| A. | -0.6 | B. | -0.69 | C. | -0.7 | D. | -0.71 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{3}$,$\frac{2\sqrt{2}}{3}$] | B. | [$\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{2}}{3}$] | C. | [$\frac{2\sqrt{2}}{3}$,1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.
某高校调查了400名大学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25)[25,27.5),[27.5,30].根据此直方图,这400名大学生中每周的自习时间不少于25小时的人数是120.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
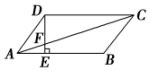
| A. | 54 cm2 | B. | 24 cm2 | C. | 18 cm2 | D. | 12 cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com