练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲乙两队进行排球比赛，已知每一局比赛中甲队获胜的概率是，没有平局．采用三局两胜制比赛，即先胜两局者获胜且比赛结束，则甲队获胜的概率等于（　　）

    A．B．C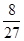．D．

    A

    解析试题分析：比赛两局甲获胜：；比赛3局甲获胜,则前两句甲胜其中一局，第三局甲胜：
    ，所以甲获胜的概率
    考点：独立重复试验与相互独立事件同时发生
    点评：正确求解本题的首要条件是分析清楚甲获胜的方案，特别是比赛3局时，假在前两局只能胜1局

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于

    A． B．
    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    对同一目标进行两次射击，第一、二次射击命中目标的概率分别为和，则两次射击中至少有一次命中目标的概率是（  ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设随机变量，若，则的值为(　　)

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    将一颗骰子抛掷两次，所得向上点数分别为，则函数在上为增函数的概率是   （     ）

    A． B． C． D． 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    两个实习生每人加工一个零件，加工为一等品的概率分别为和，两个零件是否加工为一等品相互独立，则这两个零件中恰好有一个一等品的概率为（   ）

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    小强和小华两位同学约定下午在大良钟楼公园喷水池旁见面,约定谁先到后必须等10分钟,这时若另一人还没有来就可以离开.如果小强是1：40分到达的,假设小华在1点到2点内到达,且小华在1点到2点之间何时到达是等可能的,则他们会面的概率是

    A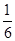．B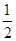．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图，在圆心角为直角的扇形OAB中，分别以OA、OB为直径作两个半圆．向
    直角扇形OAB内随机取一点，则该点刚好来自阴影部分的概率是

    A．     B．        C．     D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    电子钟一天显示的时间是从00:00到23:59的每一时刻都由四个数字组成，则一天中任一时刻的四个数字之和为23的概率为

    A． B． C． D．

    查看答案和解析>>

    同步练习册答案