Question

在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如下图所示).将矩形折叠,使A点落在线段DC上.

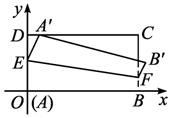
(1)若折痕所在直线的斜率为k,试写出折痕所在直线的方程;

(2)求折痕的长的最大值.

Answer 1

解:(1)设折叠后A在DC边上对应的点为A′,则折痕EF所在直线的斜率k≤0.

    当k=0时,A′与D重合,EF所在直线方程为y=.

    当k＜0时,EF垂直平分OA′.

    故直线OA′的方程为y=-x,则当A′与C重合时k=-2.

    设OA′交EF于G点,则G点坐标为(-,),得EF所在直线的方程为y=kx+.

(2)由(1)得线段EF的方程为y=kx+(-2≤k≤0).                  (*)

    当E与D重合时,E点坐标为(0,1),由(*)式得k=-1.

    当F与B重合时,F点坐标为(2,0),由(*)式得k=-2+.

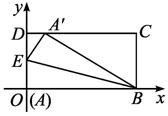
    ①当-2+≤k≤0时,E在OD上,F在BC上.

    由(*)式得E(0,)、F(2,).

    令l=|EF|²,则l=4k²+4(-2+≤k≤0)是k的减函数.

    此时l≤l(-2+)=32-16.

②当-1≤k≤-2+时,E在OD上,F在OB上.

    于是由(*)式得E(0,)、F(-,0).

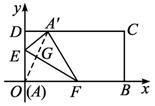
    则l=|EF|²=()²+()²=.l_k′=.

    令l_k′=02k²-1=0k=-.

    当-1≤k＜-时,l_k′＜0,则l是k的减函数.

    此时l≤l(-1)=2.

    当-＜k≤-2+时,l_k′＞0,则l是k的增函数.

    此时l≤l(-2+)=32-16.(可由①直接得到)

③当-2≤k≤-1时,E在DC上,F在OB上.

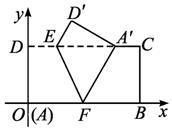
    由(*)式得E(,1)、F(-,0),

    则l=|EF|²=+1(-2≤k≤-1)是k的增函数.

    此时l≤l(-1)=2.(可由②直接得到)

    综上所述,l=|EF|²的最大值为l(-1)和l(-2+)中的最大者.

    因32-16=16(2-)＞16(2-1.75)=4,故l=32-16.

    所以折痕EF的最大值为.