
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 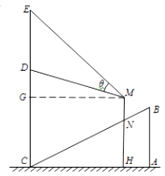
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
【答案】
(1)解:由题意可知MG=CH=x,
由△CHN∽△CAB可得 ![]() ,即
,即 ![]() ,
,
∴NH= ![]() ,
,
∴M到地面的距离MH=MN+NH= ![]()
(2)解:DG=CD﹣CG=CD﹣MH=5﹣ ![]() ,
,
同理EG=9﹣ ![]() ,
,
∴tan∠DMG= ![]() =
= ![]() ,tan∠EMG=
,tan∠EMG= ![]() ,
,
∴tanθ=tan(∠EMG﹣∠DMG)= 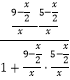 =
= ![]() =
= ![]() ,
,
∵0<x≤8,∴5x+ ![]() ≥2
≥2 ![]() =60,当且仅当5x=
=60,当且仅当5x= ![]() 即x=6时取等号,
即x=6时取等号,
∴tanθ≤ ![]() =
= ![]() ,
,
∴当x=6时,tanθ取得最大值,即θ取得最大值
【解析】(1)根据相似三角形得出NH,从而得出MH;(2)计算DG,EG,得出tan∠DMG和tan∠EMG,利用差角公式计算tanθ,得出tanθ关于x的解析式,利用不等式求出tanθ取得最大值时对应的x即可.


科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)都是定义在R上的函数,且满足以下条件:
①f(x)=axg(x)(a>0,a≠1);
②g(x)≠0;
③f(x)g'(x)>f'(x)g(x);
若 ![]() ,则a= .
,则a= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图(图1)及三视图(图2)如图所示,其中M,N分别是AF,BC的中点 
(1)求证:MN∥平面CDEF:
(2)求二面角A﹣CF﹣B的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点P在正方体ABCD﹣A1B1C1D1的面对角线BC1上运动,则下列四个结论:
①三棱锥A﹣D1PC的体积不变;
②A1P∥平面ACD1;
③DP⊥BC1;
④平面PDB1⊥平面ACD1 .
其中正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
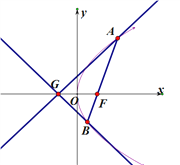
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解下列各题:
(1)求下列椭圆5x2+9y2=100的焦点和顶点的坐标;
(2)求抛物线 y2﹣6x=0的焦点坐标,准线方程和对称轴;
(3)求焦点在x轴上,两顶点间的距离是8,e= ![]() 的 双曲线的标准方程.
的 双曲线的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com