
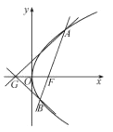
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
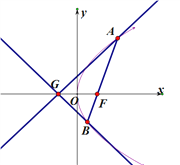
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析
;(Ⅱ)详见解析
【解析】试题分析:解法一:(Ⅰ)由抛物线的定义得![]() .因为
.因为![]() ,即
,即![]() ,解得
,解得![]() ,即可求出抛物线
,即可求出抛物线![]() 的方程.(Ⅱ)因为点
的方程.(Ⅱ)因为点![]() 在抛物线
在抛物线![]()
![]() 上,所以
上,所以![]() ,由抛物线的对称性,不妨设
,由抛物线的对称性,不妨设![]() .由
.由![]() ,
, ![]() 可得直线
可得直线![]() 的方程为
的方程为![]() .由
.由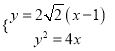 ,得
,得![]() ,从而
,从而![]() . 所以
. 所以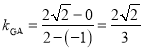 ,
, 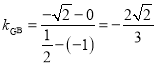 ,所以
,所以![]() ,从而
,从而![]() ,这表明点
,这表明点![]() 到直线
到直线![]() ,
, ![]() 的距离相等,即可证明结果.
的距离相等,即可证明结果.
解法二:(Ⅱ)同解法一可得,直线![]() 的方程为
的方程为![]() ,
,
从而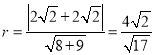 .又直线
.又直线![]() 的方程为
的方程为![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离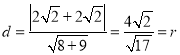 ,即可证明结果.
,即可证明结果.
试题解析:解法一:(Ⅰ)由抛物线的定义得![]() .
.
因为![]() ,即
,即![]() ,解得
,解得![]() ,所以抛物线
,所以抛物线![]() 的方程为
的方程为![]() .
.
(Ⅱ)因为点![]() 在抛物线
在抛物线![]()
![]() 上,
上,
所以![]() ,由抛物线的对称性,不妨设
,由抛物线的对称性,不妨设![]() .
.
由![]() ,
, ![]() 可得直线
可得直线![]() 的方程为
的方程为![]() .
.
由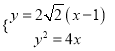 ,得
,得![]() ,
,
解得![]() 或
或![]() ,从而
,从而![]() .
.
又![]() ,
,
所以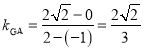 ,
,  ,
,
所以![]() ,从而
,从而![]() ,这表明点
,这表明点![]() 到直线
到直线![]() ,
, ![]() 的距离相等,
的距离相等,
故以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆必与直线
相切的圆必与直线![]() 相切.
相切.
解法二:(Ⅰ)同解法一.
(Ⅱ)设以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的半径为
相切的圆的半径为![]() .
.
因为点![]() 在抛物线
在抛物线![]()
![]() 上,
上,
所以![]() ,由抛物线的对称性,不妨设
,由抛物线的对称性,不妨设![]() .
.
由![]() ,
, ![]() 可得直线
可得直线![]() 的方程为
的方程为![]() .
.
由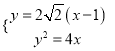 ,得
,得![]() ,
,
解得![]() 或
或![]() ,从而
,从而![]() .
.
又![]() ,故直线
,故直线![]() 的方程为
的方程为![]() ,
,
从而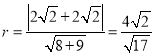 .
.
又直线![]() 的方程为
的方程为![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离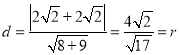 .
.
这表明以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆必与直线
相切的圆必与直线![]() 相切.
相切.


科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 上一动点,
上一动点,![]() 轴于点
轴于点![]() ,若动点
,若动点![]() 满足
满足![]() (其中
(其中![]() 为非零常数)
为非零常数)
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)当![]() 时,得到动点
时,得到动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,斜率为
,斜率为![]() 1的直线
1的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果不等式ax2+bx+c>0的解集为{x|﹣2<x<4},那么对于函数f(x)=ax2+bx+c应有( )
A.f(5)<f(2)<f(﹣1)
B.f(﹣1)<f(5)<f(2)
C.f(2)<f(﹣1)<f(5)
D.f(5)<f(﹣1)<f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 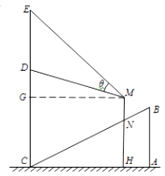
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年7月16日,中国互联网络信息中心发布《第三十四次中国互联网发展状况报告》,报告显示:我国网络购物用户已达![]() 亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为
亿.为了了解网购者一次性购物金额情况,某统计部门随机抽查了6月1日这一天100名网购者的网购情况,得到如下数据统计表.已知网购金额在2000元以上(不含2000元)的频率为![]() .
.

(Ⅰ)确定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(Ⅱ)为进一步了解网购金额的多少是否与网龄有关,对这100名网购者调查显示:购物金额在2000元以上的网购者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的网购者中网龄不足3年的有20人.
①请将列联表补充完整;
网龄3年以上 | 网龄不足3年 | 合计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
合计 | 100 |
②并据此列联表判断,是否有![]() %的把握认为网购金额超过2000元与网龄在三年以上有关?
%的把握认为网购金额超过2000元与网龄在三年以上有关?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 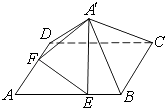
(1)求五棱锥A′﹣BCDFE的体积;
(2)求平面A′EF与平面A′BC的夹角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车4s店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 | a | 10 | b |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值.
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及数学期望EY.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人投篮命中的概率为别为 ![]() 与
与 ![]() ,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1个的概率;
(2)设ξ表示比赛结束后,甲、乙两人进球数的差的绝对值,求ξ的概率分布和数学期望E(ξ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com