
【题目】某品牌汽车4s店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
频数 | 40 | 20 | a | 10 | b |
已知分3期付款的频率为0.2,4s店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元,分2期或3期付款其利润为1.5万元,分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值.
(2)若以频率作为概率,求事件A:“购买该品牌汽车的3位顾客中,至多有一位采用3期付款”的概率P(A)
(3)求Y的分布列及数学期望EY.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)分布列略,
;(3)分布列略,![]() .
.
【解析】
试题分析:(1)根据分3期付款的频率为0.2,得到![]() 除以100的值为0.2,求出
除以100的值为0.2,求出![]() 的值,再根据总体数是100,求出
的值,再根据总体数是100,求出![]() 的值;
的值;
(2)记分期付款的期数为![]() ,则
,则![]() 的可能取值是1,2,3,4,5,结合变量对应事件写出变量的概率,根据独立重复试验的概率公式得到购买该品牌汽车的3位顾客中至多1位采用3期付款的概率;
的可能取值是1,2,3,4,5,结合变量对应事件写出变量的概率,根据独立重复试验的概率公式得到购买该品牌汽车的3位顾客中至多1位采用3期付款的概率;
(3)记![]() 表示经销一辆汽车的利润,
表示经销一辆汽车的利润,![]() 的可能取值为1,1.5,2,结合变量对应的事件,根据
的可能取值为1,1.5,2,结合变量对应的事件,根据![]() 和
和![]() 之间的关系,写出变量的概率,得出分布列.
之间的关系,写出变量的概率,得出分布列.
试题解析:(1)![]()
![]()
![]()
![]()
(2)记分期付款的期数为![]() ,则:
,则:![]() ,
,![]() ,
,![]()
![]()
![]() ,故所求概率
,故所求概率![]()
(3)Y可能取值为1,1.5,2(万元) ![]()
![]() ,
,![]()
![]() Y的分布列为:
Y的分布列为:
Y | 1 | 1.5 | 2 |
P | 0.4 | 0.4 | 0.2 |
Y的数学期望![]() (万元)
(万元)


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1, ![]() ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
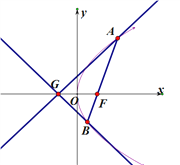
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,左顶点为
轴上,左顶点为![]() ,左焦点为
,左焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)以![]() 为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
为直径的圆是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解下列各题:
(1)求下列椭圆5x2+9y2=100的焦点和顶点的坐标;
(2)求抛物线 y2﹣6x=0的焦点坐标,准线方程和对称轴;
(3)求焦点在x轴上,两顶点间的距离是8,e= ![]() 的 双曲线的标准方程.
的 双曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别是
的左右焦点分别是![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,当
,当![]() 时,
时, ![]() 恰为椭圆
恰为椭圆![]() 的上顶点,此时
的上顶点,此时![]() 的面积为6.
的面积为6.

(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() ,问当
,问当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
轴截得的弦长是否为定值?若是,求出这个定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某港湾的平面示意图如图所示, ![]() ,
, ![]() ,
, ![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向6km处,
的正南方向6km处, ![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向10km处.
方向10km处.
(Ⅰ)求集镇![]() ,
, ![]() 间的距离;
间的距离;
(Ⅱ)随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上航线.勘测时发现:以
,开辟水上航线.勘测时发现:以![]() 为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头
为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头![]() 的位置,使得
的位置,使得![]() 之间的直线航线最短.
之间的直线航线最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 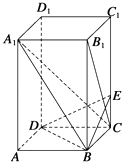
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com