Question

【题目】已知函数fn（x）=a1x+a2x2+a3x3+…+anxn ， 且fn（﹣1）=（﹣1）nn，n∈N* ， 设函数g（n）= ，若bn=g（2n+4），n∈N* ， 则数列{bn}的前n（n≥2）项和Sn等于 ．

Answer 1

【答案】2n+n﹣1
【解析】解：由函数g（n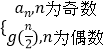）= ， 可得bn=g（2n+4）=g（2n﹣1+2）=g（2n﹣2+1）=a ，
由函数fn（x）=a1x+a2x2+a3x3+…+anxn ， 且fn（﹣1）=（﹣1）nn，
可得﹣a1+a2﹣a3+…+an（﹣1）n=（﹣1）nn，①
n=1时，﹣a1=﹣1，可得a1=1；
n≥2时，﹣a1+a2﹣a3+…+an﹣1（﹣1）n﹣1=（﹣1）n﹣1（n﹣1），②
①﹣②可得an（﹣1）n=（﹣1）nn﹣（﹣1）n﹣1（n﹣1），
化简可得an=2n﹣1，对n=1也成立．
则bn=a =2n﹣1+1，
则数列{bn}的前n（n≥2）项和Sn等于（1+2+4+…+2n﹣1）+n
= +n=2n+n﹣1．
所以答案是：2n+n﹣1．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系．