
分析 根据所给的二项式,利用二项展开式的通项公式写出第r+1项,令$\frac{1}{x}$的指数为2求得r,再代入系数求出结果.
解答 解:根据所给的二项式写出展开式的通项为,
Tr+1=${C}_{5}^{r}$•${(\frac{1}{x})}^{5-r}$•(-2)r,
要求含$\frac{1}{{x}^{2}}$项的系数,
令5-r=2,
解得r=3,
所以含$\frac{1}{{x}^{2}}$项的系数是${C}_{5}^{3}$•(-2)3=-80.
故答案为:-80.
点评 本题考查二项式定理的应用问题,解题的关键是正确写出二项展开式的通项,在这种题目中通项是解决二项展开式的特定项问题的工具.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.
设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
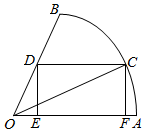 圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?
圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
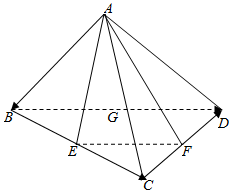 如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com