
分析 (Ⅰ)由抛物线y2=4x的焦点与椭圆C的一个焦点重合,且椭圆C短轴的一个端点和两个焦点构成直角三角形,得到b=c=1,由此能求出椭圆C的方程.
∴“相关圆”E的方程为x2+y2=$\frac{2}{3}$.
(Ⅱ)当直线l的斜率不存在时,直线AB方程为x=$\frac{\sqrt{6}}{3}$,$∠AOB=\frac{π}{2}$;当直线l的斜率存在时,设其方程为y=kx+m,代入椭圆方程,得x2+2(kx+m)2=2,由此利用根的判别式、韦达定理、直线与圆相切,结合已知条件推导出$∠AOB=\frac{π}{2}$为定值.
(ii)要求△ABQ的面积的取值范围,只需求弦长|AB|的范围,由此利用椭圆弦长公式能求出△ABQ面积的取值范围.
解答 解:(Ⅰ)∵抛物线y2=4x的焦点与椭圆C的一个焦点重合,
且椭圆C短轴的一个端点和两个焦点构成直角三角形,
∴b=c=1,∴a2=1+1=2,
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.
∴“相关圆”E的方程为x2+y2=$\frac{2}{3}$.
证明:(Ⅱ)(i)当直线l的斜率不存在时,不妨设直线AB方程为x=$\frac{\sqrt{6}}{3}$,
则A($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),B($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),∴$∠AOB=\frac{π}{2}$,
当直线l的斜率存在时,设其方程为y=kx+m,设A(x1,y1),B(x2,y2),
联立方程组$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得x2+2(kx+m)2=2,
即(1+2k2)x2+4kmx+2m2-2=0,
△=16k2m2-4(1+2k2)(2m2-2)=8(2k2-m2+1)>0,
即2k2-m2+1>0,(*)
$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-\frac{4km}{1+2{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{2{m}^{2}-2}{1+2{k}^{2}}}\end{array}\right.$,
∵直线与圆相切,
∴$d=\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{\frac{{m}^{2}}{1+{k}^{2}}}$=$\sqrt{\frac{2}{3}}$,∴3m2=2+2k2,
∴${x}_{1}{x}_{2}+{y}_{1}{y}_{2}=(1+{k}^{2}){x}_{1}{x}_{2}$+km(x1+x2)+m2
=$\frac{(1+{k}^{2})(2{m}^{2}-2)}{1+2{k}^{2}}-\frac{4{k}^{2}{m}^{2}}{1+2{k}^{2}}+{m}^{2}$
=$\frac{3{m}^{2}-2{k}^{2}-2}{1+2{k}^{2}}$=0,
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$,
∴$∠AOB=\frac{π}{2}$为定值.
解:(ii)∵PQ是“相关圆”的直径,
∴${S}_{△ABQ}=\frac{1}{2}|AB||PQ|=\frac{\sqrt{6}}{3}|AB|$,
∴要求△ABQ的面积的取值范围,只需求弦长|AB|的范围,
当直线AB的斜率不存在时,由(i)知|AB|=$\frac{2\sqrt{6}}{3}$,
|AB|=$\sqrt{(1+{k}^{2})({x}_{1}-{x}_{2})^{2}}$=$\sqrt{(1+{k}^{2})•\frac{8(2{k}^{2}-{m}^{2}+1)}{(1+2{k}^{2})^{2}}}$
=$\sqrt{\frac{8}{3}•\frac{4{k}^{4}+5{k}^{2}+1}{4{k}^{4}+4{k}^{2}+1}}$=$\sqrt{\frac{8}{3}[1+\frac{{k}^{2}}{4{k}^{4}+4{k}^{2}+1}]}$,
①当k≠0时,|AB|=$\sqrt{\frac{8}{3}(1+\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4})}$,
∵$4{k}^{2}+\frac{1}{{k}^{2}}+4≥8$,∴0<$\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4}$$≤\frac{1}{8}$,
∴$\frac{8}{3}<\frac{8}{3}(1+\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+1})$≤3,
∴$\frac{2}{3}\sqrt{6}$<|AB|$≤\sqrt{3}$,
当且仅当k=$±\frac{\sqrt{2}}{2}$时,取“=”号.
②当k=0时,|AB|=$\frac{2\sqrt{6}}{3}$.|AB|的取值范围为$\frac{2}{3}\sqrt{6}$≤|AB|$≤\sqrt{3}$,
∴△ABQ面积的取值范围是[$\frac{4}{3}$,$\sqrt{2}$].
点评 本题考查椭圆方程的求法,考查相关圆的方程的求法,考查角为定值的与求法,考查三角形面积的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、直线与圆相切、椭圆弦长公式的合理运用.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
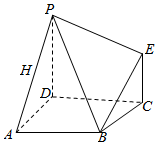 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
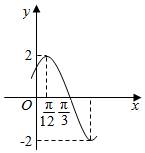 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | ω=2,φ=$\frac{π}{6}$ | |
| B. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m的取值范围是(-2,-$\sqrt{3}$] | |
| D. | 将函数y=2cos(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{12}$的单位得到函数f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{24}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{48}{49}$ | D. | $\frac{63}{64}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com