Question

5．已知平面内有三个向量$\overrightarrow{OA}，\overrightarrow{OB}，\overrightarrow{OC}$，其中∠AOB=60°，∠AOC=30°，且$|\overrightarrow{OA}|=2$，$|\overrightarrow{OB}|=2$，$|\overrightarrow{OC}|=4\sqrt{3}$，若$\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}（λ，μ∈R）$，则λ+μ=4或2．

Answer 1

分析 以OC为对角线，以OA，OB方向为邻边作平行四边形，求出平行四边形OA方向上的边长即可得出答案

解答 解：①当OB，OC在OA同侧时，
过点C作CE∥OB交OA的延长线于点E，过点C作CF∥OA交OB的延长线于点F，
则$\overrightarrow{OC}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$．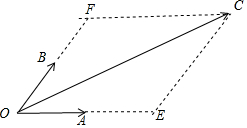

∵∠AOB=60°，∠AOC=30°，
∴∠OCE=∠COF=∠COE=30°，$|\overrightarrow{OC}|=4\sqrt{3}$，
∴|$\overrightarrow{CE}$|=|$\overrightarrow{OE}$|=4，
∵$|\overrightarrow{OA}|=2$，$|\overrightarrow{OB}|=2$，
∴λ=μ=2，
∴λ+μ=4．
②当OB，OC在OA同侧时，
过点C作CE∥OB交OA的延长线于点E，过点C作CF∥OA交OB的延长线于点F，
则$\overrightarrow{OC}$=$\overrightarrow{OE}$+$\overrightarrow{OF}$．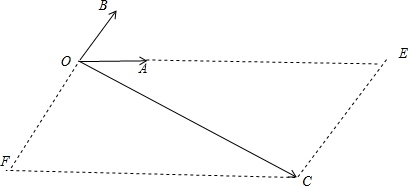

∵∠AOB=60°，∠AOC=30°，
∴∠OCE=∠COF=90°，∠COE=30°，$|\overrightarrow{OC}|=4\sqrt{3}$，
∴|$\overrightarrow{CE}$|=4，|$\overrightarrow{OE}$|=8，
∵$|\overrightarrow{OA}|=2$，$|\overrightarrow{OB}|=2$，
∴λ=4，μ=-2，
∴λ+μ=2．
故答案为：4或2

点评 本题考查了向量在几何中的应用，平面向量的基本定理，向量运算的几何意义，属于中档题