
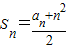 .
.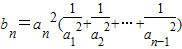 ,证明:当n≥2时,
,证明:当n≥2时,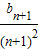
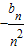 =
=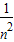 ;
;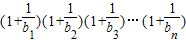 与4的大小关系.
与4的大小关系.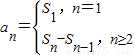 及其等差数列的通项公式即可得出;
及其等差数列的通项公式即可得出; ,
,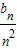 的表达式,相减即可得出;
的表达式,相减即可得出;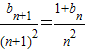 ,可得
,可得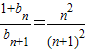 .利用(2)及“累乘求积”、“放缩法”、“裂项求和”即可得出.
.利用(2)及“累乘求积”、“放缩法”、“裂项求和”即可得出.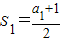 ,∴a1=1,)
,∴a1=1,)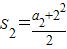 ,∴a2=2,
,∴a2=2,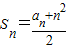 ,
,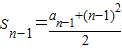 ,
,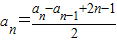
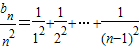 ①
① ②
②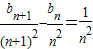 .
.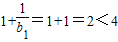 ,当n=2时,
,当n=2时,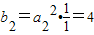
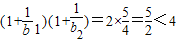
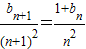 ,∴
,∴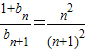
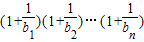 =
=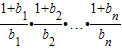
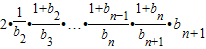
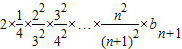
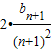
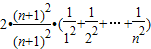
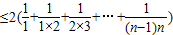 =
=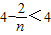 .
.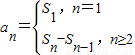 及其等差数列的通项公式求an、变形利用“累乘求积”、“放缩法”、“裂项求和”等方法是解题的关键.
及其等差数列的通项公式求an、变形利用“累乘求积”、“放缩法”、“裂项求和”等方法是解题的关键. 

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com