
【题目】已知△ABC内角A,B,C的对边分别是a,b,c,且![]() .
.
(Ⅰ)求A;
(Ⅱ)若![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】为响应国家“节能减排,开发清洁能源”的号召,小华制作了一个太阳灶,如图所示.集光板由抛物面(抛物线绕对称轴旋转得到)形的反光镜构成,已知镜口圆的直径为![]() ,镜深
,镜深![]() ,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点( )
,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点( )
A.0.5米B.1米C.1.5米D.2米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用“健步行![]() ” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为
” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() 九组,整理得到如图频率分布直方图:
九组,整理得到如图频率分布直方图:
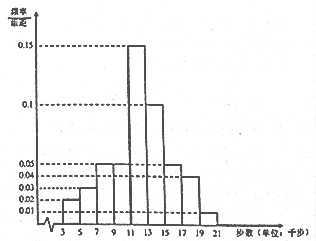
(1)求当天这1000名会员中步数少于11千步的人数;
(2)从当天步数在![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(3)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.

(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径:一种是从A处沿直线步行到C处;另一种是先从A处沿索道乘缆车到B处,然后从B处沿直线步行到C处,现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m·min-1.在甲出发2 min后,乙从A处乘缆车到B处,在B处停留1 min后,再从B处匀速步行到C处假设缆车的速度为130 m·min-1,山路AC长为1260 m,经测量![]() ,
,![]() .
.

(1)乙出发多长时间后,乙在缆车上与甲的距离最短?
(2)为使甲、乙在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从7名男生和5名女生中选出5人,分别求符合下列条件的选法数.
(1)![]() ,
,![]() 必须被选出;
必须被选出;
(2)至少有2名女生被选出;
(3)让选出的5人分别担任体育委员、文娱委员等5种不同职务,但体育委员由男生担任,文娱委员由女生担任.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为Body Mass Index,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方. 根据中国肥胖问题工作组标准,当BMI![]() 时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:
时为肥胖. 某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,得到被调查者的频率分布直方图如图:

(1)求被调查者中肥胖人群的BMI 平均值![]() ;
;
(2)根据频率分布直方图,完成下面的![]() 列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
列联表,并判断能有多大(百分数)的把握认为 35 岁以上成人高血压与肥胖有关?
肥胖 | 不肥胖 | 总计 | |
高血压 | |||
非高血压 | |||
总计 |
参考公式: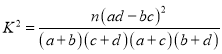 ,其中
,其中![]() .
.
参考数据:
| 0.25 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com