Question

8．如图正三棱柱ABC-A₁B₁C₁中，底面边长为a，侧棱长为$\frac{{\sqrt{2}}}{2}a$，若经过对角线AB₁且与对角线BC₁平行的平面交上底面于DB₁．
（1）试确定D点的位置，并证明你的结论；
（2）求二面角A₁-AB₁-D的大小．

Answer 1

分析 （1）连结A₁B与AB₁交于E，DE为平面AB₁D与平面A₁BC₁的交线，推导出BC₁∥DE，由此能证明D为A₁C₁的中点．
（2）过D作DF⊥A₁B₁于F，连结EF，DE，推导出∠DEF为二面角A₁-AB₁-D的大小，由此能求出结果．

解答 解：（1）D为A₁C₁的中点．连结A₁B与AB₁交于E，
则E为A₁B的中点，DE为平面AB₁D与平面A₁BC₁的交线，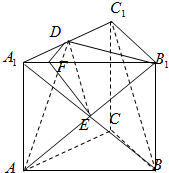
∵BC₁∥平面AB₁D
∴BC₁∥DE，∴D为A₁C₁的中点．
（2）过D作DF⊥A₁B₁于F，由正三棱柱的性质，AA₁⊥DF，
∴DF⊥平面AB₁，连结EF，DE，在正△A₁B₁C₁中，
∵D是A₁C₁的中点，∴${B_1}D=\frac{{\sqrt{3}}}{2}{A_1}{B_1}=\frac{{\sqrt{3}}}{2}a$，
又在直角三角形AA₁D中，$AD=\sqrt{AA_1^2+{A_1}{D^2}}=\frac{{\sqrt{3}}}{2}a$，
∴AD=B₁D．∴DE⊥AB₁，
∴EF⊥AB₁．∴∠DEF为二面角A₁-AB₁-D的大小，
由题意$DF=\frac{{\sqrt{3}}}{4}a$，∵△B₁FE∽△B₁AA₁，∴$EF=\frac{{\sqrt{3}}}{4}a$，∴$∠DEF=\frac{π}{4}$．
∴二面角A₁-AB₁-D的大小为$\frac{π}{4}$．

点评 本题考查空间位置关系的判断与证明，考查二面角的求法，考查空间想象能力、推理论证能力和运算求解能力，是中档题．