
【题目】如图所示,异面直线![]() ,
,![]() 互相垂直,
互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,截面
,截面![]() 分别与
分别与![]() ,
,![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
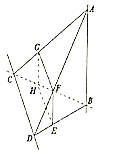
(1)求证:![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的正切值.
的正切值.
【答案】(1)见解析(2)![]()
【解析】分析:(1)推导出AB∥EF,CD∥HE,AB⊥BC,BC⊥DC,BC⊥EF,BC⊥EH,由此能证明BC⊥平面EFGH.
(2)作![]() ,以C为原点,CD为x轴,CB为y轴,Cz为z轴,建立空间直角坐标系C﹣xyz,利用向量法能求出二面角B﹣AD﹣C的正切值.
,以C为原点,CD为x轴,CB为y轴,Cz为z轴,建立空间直角坐标系C﹣xyz,利用向量法能求出二面角B﹣AD﹣C的正切值.
详解:(1)∵![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
∴![]() ,同理
,同理![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
同理![]() .
.
∴![]() ,同理
,同理![]() .
.
又∵![]() ,
,![]() 是平面
是平面![]() 内的两相交直线.
内的两相交直线.
∴![]() 平面
平面![]() .
.
(2)由(1)及异面直线![]() ,
,![]() 互相垂直知,直线
互相垂直知,直线![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
作![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示,
,如图所示,
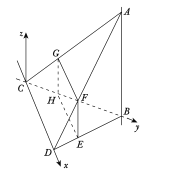
则![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() 轴
轴![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量可设为
的一个法向量可设为![]() ,
,
∵![]() ,∴
,∴![]() .
.
得![]() ,即
,即![]() ,
,
又∵![]() 轴
轴![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量可设为
的一个法向量可设为![]() .
.
∴![]() ,得
,得![]() ,即
,即![]() ,
,
设锐二面角![]() 的大小为
的大小为![]() ,
,
那么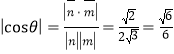 ,
,
∴![]()
∴二面角![]() 的正切值为
的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即![]() .设函数
.设函数![]() ,二次函数
,二次函数![]() ,若函数
,若函数![]() 与
与![]() 的图象有且只有一个公共点,则
的图象有且只有一个公共点,则![]() 的取值不可能是( )
的取值不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上一动点,过直线
上一动点,过直线![]() 的平面分别与棱
的平面分别与棱![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,则下列结论正确的是__________.
,则下列结论正确的是__________.
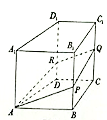
①对于任意的点![]() ,都有
,都有![]()
②对于任意的点![]() ,四边形
,四边形![]() 不可能为平行四边形
不可能为平行四边形
③存在点![]() ,使得
,使得![]() 为等腰直角三角形
为等腰直角三角形
④存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高二年级举办了一次数学史知识竞赛活动,共有![]() 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为![]() 分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:
分)进行统计,统计结果见下表.请你根据频率分布表解答下列问题:

(1)填出频率分布表中的空格;
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于![]() 分的同学能获奖,请估计在参加的
分的同学能获奖,请估计在参加的![]() 名学生中大概有多少名学生获奖?
名学生中大概有多少名学生获奖?
(3)在上述统计数据的分析中有一项计算见算法流程图,求输出的![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市根据地理位置划分成了南北两区,为调查该市的一种经济作物![]() (下简称
(下简称![]() 作物)的生长状况,用简单随机抽样方法从该市调查了 500 处
作物)的生长状况,用简单随机抽样方法从该市调查了 500 处 ![]() 作物种植点,其生长状况如表:
作物种植点,其生长状况如表:

其中生长指数的含义是:2 代表“生长良好”,1 代表“生长基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,绝收”.
(1)估计该市空气质量差的![]() 作物种植点中,不绝收的种植点所占的比例;
作物种植点中,不绝收的种植点所占的比例;
(2)能否有 99%的把握认为“该市![]() 作物的种植点是否绝收与所在地域有关”?
作物的种植点是否绝收与所在地域有关”?
(3)根据(2)的结论,能否提供更好的调查方法来估计该市![]() 作物的种植点中,绝收种植点的比例?请说明理由.
作物的种植点中,绝收种植点的比例?请说明理由.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有高三文科学生1000人,统计其高三上期期中考试的数学成绩,得到频率分布直方图如下:
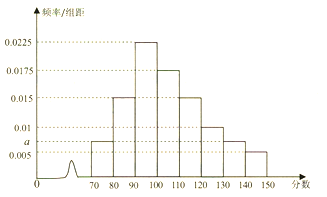
(1)求出图中![]() 的值,并估计本次考试低于120分的人数;
的值,并估计本次考试低于120分的人数;
(2)假设同组的每个数据可用该组区间的中点值代替,试估计本次考试不低于120分的同学的平均数(其结果保留一位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
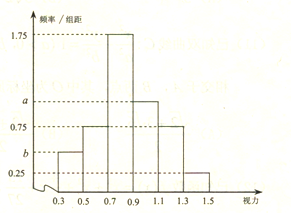
【题目】从某校高三年级中随机抽取100名学生,对其高校招生体检表中的视图情况进行统计,得到如图所示的频率分布直方图,已知从这100人中随机抽取1人,其视力在![]() 的概率为
的概率为![]() .
.
(1)求![]() 的值;
的值;
(2)若某大学![]() 专业的报考要求之一是视力在0.9以上,则对这100人中能报考
专业的报考要求之一是视力在0.9以上,则对这100人中能报考![]() 专业的学生采用按视力分层抽样的方法抽取8人,调查他们对
专业的学生采用按视力分层抽样的方法抽取8人,调查他们对![]() 专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学
专业的了解程度,现从这8人中随机抽取3人进行是否有意向报考该大学![]() 专业的调查,记抽到的学生中视力在
专业的调查,记抽到的学生中视力在![]() 的人数为
的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com