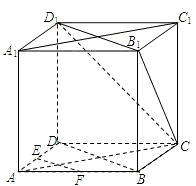
解:(Ⅰ)证明:连接BD.
在正方体AC
1中,对角线BD∥B
1D
1.
又因为E、F为棱AD、AB的中点,
所以EF∥BD.
所以EF∥B
1D
1.(4分)
又B
1D
1?平面CB
1D
1,EF?平面CB
1D
1,
所以EF∥平面CB
1D
1.(7分)
(Ⅱ)因为在长方体AC
1中,
AA
1⊥平面A
1B
1C
1D
1,而B
1D
1?平面A
1B
1C
1D
1,
所以AA
1⊥B
1D
1.(10分)
又因为在正方形A
1B
1C
1D
1中,A
1C
1⊥B
1D
1,
所以B
1D
1⊥平面CAA
1C
1.(12分)
又因为B
1D
1?平面CB
1D
1,
所以平面CAA
1C
1⊥平面CB
1D
1.(14分)
分析:(Ⅰ)欲证EF∥平面CB
1D
1,根据直线与平面平行的判定定理可知只需证EF与平面CB
1D
1内一直线平行,连接BD,根据中位线可知EF∥BD,则EF∥B
1D
1,又B
1D
1?平面CB
1D
1,EF?平面CB
1D
1,满足定理所需条件;
(Ⅱ)欲证平面CAA
1C
1⊥平面CB
1D
1,根据面面垂直的判定定理可知在平面CB
1D
1内一直线与平面CAA
1C
1垂直,而AA
1⊥平面A
1B
1C
1D
1,B
1D
1?平面A
1B
1C
1D
1,则AA
1⊥B
1D
1,A
1C
1⊥B
1D
1,满足线面垂直的判定定理则B
1D
1⊥平面CAA
1C
1,而B
1D
1?平面CB
1D
1,满足定理所需条件.
点评:本题主要考查线面平行的判定定理和线面垂直的判定定理.考查对基础知识的综合应用能力和基本定理的掌握能力.

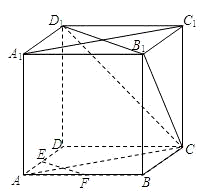 如图,在正方体ABCD-A1B1C1D1中,E、F 为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F 为棱AD、AB的中点. 解:(Ⅰ)证明:连接BD.
解:(Ⅰ)证明:连接BD.

 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则