
分析 原函数变形为y=sin2x-acosx+b=1-cos2x-acosx+b=-(cosx+$\frac{a}{2}$)2+$\frac{{a}^{2}}{4}$+b+1,根据它的最值、利用二次函数的性质、分类讨论求得a、b的值.
解答 解:原函数变形为y=sin2x-acosx+b=1-cos2x-acosx+b
=-(cosx+$\frac{a}{2}$)2+$\frac{{a}^{2}}{4}$+b+1
∵-1≤cosx≤1,a≥0
∴若0≤a≤2,当cosx=-$\frac{a}{2}$时,
ymax=1+b+$\frac{a^2}{4}$=0 ①,
当cosx=1时,ymin=-${(1+\frac{a}{2})^2}+1+b+\frac{a^2}{4}$=-a+b=-4 ②,
联立①②式解得a=2,b=-2,
y取得最大、小值时的x值分别为:x=2kπ-π(k∈Z),x=2kπ(k∈Z),
若a>2时,$\frac{a}{2}$∈(1,+∞)
∴ymax=-${(1-\frac{a}{2})^2}+1+b+\frac{a^2}{4}=a+b$=0 ③
ymin=-${(1+\frac{a}{2})^2}+1+b+\frac{a^2}{4}=-a+b=-4$④
由③④得a=2时,舍去,
综上所述a=2,b=-2,y取得最大、小值时的x值分别为:x=2kπ-π(k∈Z),x=2kπ(k∈Z),
点评 本题主要考查余弦函数的值域,二次函数的性质,体现了转化、分类讨论的数学思想,属于中档题


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
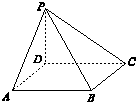 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )| A. | $\frac{1}{3}$(2-$\sqrt{2}$)m | B. | $\frac{1}{2}$(2+$\sqrt{2}$)m | C. | $\frac{1}{2}$(2-$\sqrt{2}$)m | D. | $\frac{1}{6}$(2+$\sqrt{2}$)m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-2\sqrt{2},2\sqrt{2})$ | B. | (-2,2) | C. | (-1,1) | D. | $(-\sqrt{3},\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
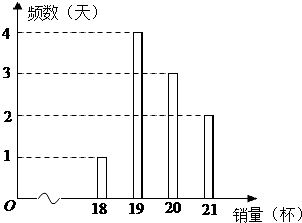 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 偏爱蔬菜 | 偏爱肉类 | 合计 | |
| 50岁以下 | 4 | 8 | 12 |
| 50岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com