
| �������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ������ | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| �������� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| ������ | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
���� ��I���衰�¼�Ai��ʾһ̨A���ھ����һ���ڳ�������ǡ��Ϊi�족�����¼�Bj��ʾһ̨B���ھ����һ���ڳ�������ǡ��Ϊj�족����i��j=1��2������7����ù�˾һ̨A���ھ����һ̨B���ھ��һ���ںϼƳ�������ǡ��Ϊ4��ĸ���ΪP��A1B3+A2B2+A3B1��=P��A1B3��+P��A2B2��+P��A3B1��=P��A1��P��B3��+P��A2��P��B2��+P��A3��P��B1����������ʼ��㼴�ɵó���
��II������Ƶ�ʿɵø��ʣ��ֱ�ó�X��Y�ķֲ��У����ɵó���ѧ������
��� �⣺��I���衰�¼�Ai��ʾһ̨A���ھ����һ���ڳ�������ǡ��Ϊi�족��
���¼�Bj��ʾһ̨B���ھ����һ���ڳ�������ǡ��Ϊj�족����i��j=1��2������7����ù�˾һ̨A���ھ����һ̨B���ھ��һ���ںϼƳ�������ǡ��Ϊ4��ĸ���ΪP��A1B3+A2B2+A3B1��=P��A1B3��+P��A2B2��+P��A3B1��=P��A1��P��B3��+P��A2��P��B2��+P��A3��P��B1��=$\frac{5}{100}��\frac{20}{100}$+$\frac{10}{100}��\frac{20}{100}$+$\frac{30}{100}��\frac{14}{100}$=$\frac{9}{125}$��
���Ըù�˾һ̨A�ͳ���һ̨B�ͳ�һ���ںϼƳ�������ǡ��Ϊ4��ĸ���Ϊ$\frac{9}{125}$��
������XΪA���ھ���������������X�ķֲ���Ϊ
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.05 | 0.10 | 0.30 | 0.35 | 0.15 | 0.03 | 0.02 |
| Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.14 | 0.20 | 0.20 | 0.16 | 0.15 | 0.10 | 0.05 |
���� ���⿼����Ƶ������ʵĹ�ϵ����������ķֲ�������ѧ������������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [1��+�ޣ� | B�� | ��0��1] | C�� | [$\frac{1}{2}$��+�ޣ� | D�� | ��0��$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2i | B�� | -i | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
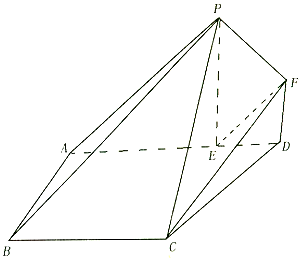 ��ͼ�����ı���ABCD�У���BAD=90�㣬AD��BC��PE��ƽ��ABCD��E��AD�ϣ�FD��PE��BC=AE=PE��DE=DF=$\frac{1}{2}$BC��
��ͼ�����ı���ABCD�У���BAD=90�㣬AD��BC��PE��ƽ��ABCD��E��AD�ϣ�FD��PE��BC=AE=PE��DE=DF=$\frac{1}{2}$BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
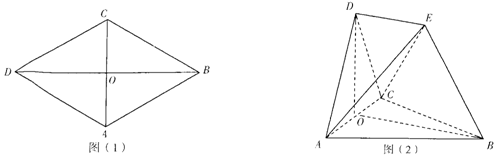
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com