在平面直角坐标系xOy中,已知圆C1:(x-3)2+(y+2)2=4,圆C2:(x+m)2+(y+m+5)2=2m2+8m+10(m∈R,且m≠-3).
(1)设P为坐标轴上的点,满足:过点P分别作圆C1与圆C2的一条切线,切点分别为T1、T2,使得PT1=PT2,试求出所有满足条件的点P的坐标;
(2)若斜率为正数的直线l平分圆C1,求证:直线l与圆C2总相交.
【答案】
分析:(1)设P为坐标轴上的点,满足:过点P分别作圆C
1与圆C
2的一条切线,切点分别为T
1、T
2,使得PT
1=PT
2,可设出P点的坐标,由直线与圆相切的性质及题设条件得到关于所引入参数的方程,解方程,有几个解,则满足条件的点P的坐标就有几个.
(2)斜率为正数的直线l平分圆C
1,故可引入参数k(>0),用待定系数法表示出直线的方程,然后求出圆心到直线的距离,与圆的半径作比较即可确定直线与圆的位置关系是相交.
解答:解:(1)由题设条件,圆C
1的圆心坐标(3,-2),半径为2,圆C
2的圆心坐标(-m,-m-5),半径为
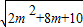
∵过点P分别作圆C
1与圆C
2的一条切线,切点分别为T
1、T
2,使得PT
1=PT
2,
∴PC
12-4=PC
22-(2m
2+8m+10)
若点P在X轴上,设P(x,0),将P(x,0)及圆心的坐标代入整理得(2m-6)x=-2m+6,故x=-1,
即P(-1,0)
若点P在Y轴上,可设P(0,y),同理解得y=-1,即P(0,-1)
故满足条件的点P的坐标为(-1,0)或(0,-1)
(2)若斜率为正数的直线l平分圆C
1,可得此直线过定点(3,-2),
设此直线的方程为y+2=k(x-3),整理得kx-y-3k-2=0
圆C
2的圆心到此直线的距离为d=
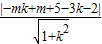
=
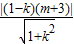
由于d
2-r
2=
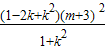
-(2m
2+8m+10)
=
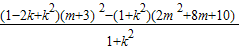
=-m
2-2m-1-
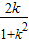
(m+3)
2=-(m+1)
2-
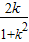
(m+3)
2<0 (∵k>0)
可得在d<r,即直线l与圆C
2总相交
点评:本题考查直线与圆的方程的应用,考查了直线与圆的位置关系转化以及以及直线与圆总相交的证明方法,一般证明直线与圆相交,只须说明直线上有一点在圆内即可,由于本题中直线斜率k为正,不是全体实数,故本题采用了用圆心到直线的距离与圆的半径相比较的方法来证明直线与圆相交,其规律是若圆心到直线的距离小于半径即可说明直线与圆相交.

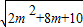
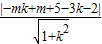 =
=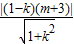
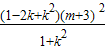 -(2m2+8m+10)
-(2m2+8m+10)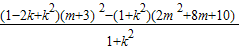
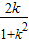 (m+3)2
(m+3)2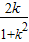 (m+3)2<0 (∵k>0)
(m+3)2<0 (∵k>0)

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是