
分析 (Ⅰ)当n≥2时,利用an=Sn-Sn-1计算、整理得an+1=2an(n≥2),进而可知数列{an}是首项、公比均为2的等比数列,计算即得结论;
(Ⅱ)通过p,q,r成等差数列可知p+r=2q,假设ap-1,aq-1,ar-1成等比数列可知(ap-1)(ar-1)=(aq-1)2,代入计算可知2p+2r=2•aq,利用基本不等式可知2p+2r>2$\sqrt{{2}^{p}•{2}^{r}}$=2•aq,从而得出矛盾.
解答 解:(Ⅰ)∵an+1=Sn+2,
∴当n≥2时,an=Sn-Sn-1=(an+1-1)-(an-2),
整理得:an+1=2an(n≥2),
又∵a2=S1+2=4=2a1满足上式,
∴数列{an}是首项、公比均为2的等比数列,
∴其通项公式an=2n;
(Ⅱ)结论:ap-1,aq-1,ar-1不成等比数列.
理由如下:
∵p,q,r成等差数列,
∴p+r=2q,
假设ap-1,aq-1,ar-1成等比数列,
则(ap-1)(ar-1)=(aq-1)2,
即(2p-1)(2r-1)=(aq-1)2,
化简得:2p+2r=2•aq,
∵p≠r,
∴2p+2r>2$\sqrt{{2}^{p}•{2}^{r}}$=2•aq,
这与假设矛盾,故假设不成立,即ap-1,aq-1,ar-1不成等比数列.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},2)∪(2,+∞)$ | B. | (2,+∞) | C. | $(-∞,-\frac{1}{2})$ | D. | $(\frac{1}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.
上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
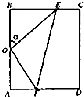 某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com