
分析 (1)求出函数的导数,求得切线的斜率,由点斜式方程可得切线的方程;
(2)由导数大于0,可得增区间;导数小于0,可得减区间,即可得到极值.
解答 解:(1)函数f(x)=x3-2x2+x+1的导数为
f′(x)=3x2-4x+1,
即有在点(2,3)处的切线斜率为12-8+1=5,
则在点(2,3)处的切线方程为y-3=5(x-2),
即为5x-y-7=0;
(2)由f′(x)>0,可得x>1或x<$\frac{1}{3}$;
由f′(x)<0,可得$\frac{1}{3}$<x<1.
可得f(x)的增区间为(1,+∞),(-∞,$\frac{1}{3}$),
减区间为($\frac{1}{3}$,1).
即有x=1处取得极小值,且为1,
x=$\frac{1}{3}$处取得极大值,且为$\frac{31}{27}$.
点评 本题考查导数的应用:求切线的方程和单调区间、极值,考查运算能力,属于基础题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
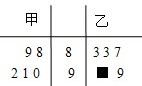 如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com