
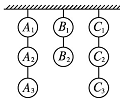
 在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?
在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序? 分析 打完8个靶子的所有不同次序相当于8个字母排序,但要求 A 1在 A 2之前,A 2在 A 3之前,B 1在 B 2之前,C 1在 C 2之前,C 2在 C 3之前,例如 B 1A 1A 2C 1B 2C 2A 3C 3,这是其中一个次序,所以这是一个定序排列问题.
解答 解:打完8个靶子的所有不同次序相当于8个字母排序,但要求 A 1在 A 2之前,A 2在 A 3之前,B 1在 B 2之前,C 1在 C 2之前,C 2在 C 3之前,例如 B 1A 1A 2C 1B 2C 2A 3C 3,这是其中一个次序,所以这是一个定序排列问题.
可设想一列有8个位置,其中选取3个位置放置 A 1、A 2、A 3,由于 A 1、A 2、A 3的次序是唯一的,所以有 C83种不同情形,从剩下5个位置中选取2个位置放置 B 1,B 2有 C52种情形,其余3个位置放置 C 1,C 2,C 3只有一种情形.
所以,击碎8个靶子的不同次序有 C83•C52=560(种).
点评 此题考查排列组合的实际运用,注意理解题意,合理利用两种计数原理解决问题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | ($\frac{2}{3}$,1) | C. | (-∞,1) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{5}$ | B. | $4\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ | B. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ | C. | $\overrightarrow a+\frac{1}{2}\overrightarrow b$ | D. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com