
分析 问题转化为y=f(x)与y=a(x-1)有且只有两个不同的交点,即可得出结论.
解答 解:设1<x≤3,则-1<x-2≤1,f(x)=$-\frac{1}{2}(x-2)^{2}+\frac{1}{2}$,同理3<x≤5,f(x)=$-\frac{1}{2}(x-4)^{2}+\frac{1}{2}$+$\frac{1}{2}$,
∵方程f(x)=a|x-1|,(a∈R)有且仅有两个不相等的实数解,
∴y=f(x)与y=a(x-1)有且只有两个不同的交点,
可知a≤0时满足题意,
a>0时,由$-\frac{1}{2}(x-4)^{2}+\frac{1}{2}$+$\frac{1}{2}$=a(x-1),可得x2+(2a-8)x-2a+14=0,
由△=(2a-8)2-4(-2a+14)=0,可得a=3-$\sqrt{7}$.
(5,$\frac{1}{2}$)代入y=a(x-1),可得a=$\frac{1}{8}$,(7,1)代入y=a(x-1),可得a=$\frac{1}{6}$,故$\frac{1}{8}≤a<\frac{1}{6}$满足题意,
∴若方程f(x)=a|x-1|,(a∈R)有且仅有两个不相等的实数解,则实数a的取值范围是a≤0或a=3-$\sqrt{7}$或$\frac{1}{8}≤a<\frac{1}{6}$.
故答案为a≤0或a=3-$\sqrt{7}$或$\frac{1}{8}≤a<\frac{1}{6}$.
点评 本题考查方程根的研究,考查数形结合的数学思想,正确运用函数的图象是关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
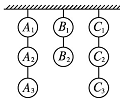 在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?
在一次射击比赛中,8个泥制的靶子挂成三列,其中两列各挂3个,一列挂2个,一射手射击时只准击碎三列靶子任一列中最下面的一个,若每次射击都遵循这条原则,则击碎8个靶子可以有多少种不同的次序?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1]∪[3,+∞) | B. | [-3,1]∪[2,+∞) | C. | [-1,1]∪[3,+∞) | D. | (-∞,-3]∪[1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
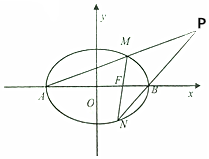 己知椭圆$\frac{x^2}{m}+\frac{y^2}{n}=1$(m>n>0)的离心率e的值为$\frac{1}{2}$,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.
己知椭圆$\frac{x^2}{m}+\frac{y^2}{n}=1$(m>n>0)的离心率e的值为$\frac{1}{2}$,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | (1,+∞) | B. | (-∞,-$\frac{3}{2}$)∪(-1,1) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x<3y | B. | lnx<lny | C. | ($\frac{1}{4}$)x>($\frac{1}{4}$)y | D. | $\frac{1}{x}$<$\frac{1}{y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com